การทำให้เป็นเส้นตรงฮาร์มอนิกขององค์ประกอบไม่เชิงเส้นวิธีนี้ใช้เพื่อศึกษาระบบไม่เชิงเส้นที่มีส่วนเชิงเส้นอยู่เหนือลำดับที่สาม ในระบบส่วนใหญ่ กระบวนการชั่วคราวคือการสั่นแบบแดมเปอร์ ดังนั้น ที่อินพุตขององค์ประกอบไม่เชิงเส้นตามแนวหลัก ข้อเสนอแนะ(GOS) สัญญาณเป็นระยะถูกส่งด้วยแอมพลิจูดที่เปลี่ยนแปลงช้าและต่อหน้าสัญญาณอินพุตพร้อมกับส่วนประกอบคงที่

เราจะถือว่าที่อินพุตขององค์ประกอบที่ไม่เชิงเส้นในช่วงเริ่มต้นขนาดเล็กช่วงหนึ่ง แอมพลิจูดและความถี่จะไม่เปลี่ยนแปลง หรือสอดคล้องกับแอมพลิจูดและความถี่ของการสั่นของระบบเอง ที่ทางออกของ NE เราได้รับ ฟังก์ชั่นเป็นระยะซึ่งสามารถขยายเป็นอนุกรมฟูริเยร์ได้ ในการศึกษาระบบไม่เชิงเส้นมักใช้เฉพาะส่วนประกอบฮาร์มอนิกแรกเท่านั้นตั้งแต่ ในกรณีส่วนใหญ่ ส่วนเชิงเส้นของระบบคือตัวกรอง ความถี่ต่ำ. แต่เพื่อตรวจสอบสิ่งนี้และการบังคับใช้ของวิธีการวิจัยนี้ จำเป็นต้องกำหนดความถี่ของการสั่นในตัวเองในระบบ ซึ่งในอนาคตจะกำหนดความสามารถของส่วนเชิงเส้นในการกรองฮาร์โมนิกที่สูงขึ้น เมื่อต้องการทำเช่นนี้ ให้สร้างการตอบสนองความถี่ของส่วนเชิงเส้น (LP)

ให้ LP ของระบบเป็นตัวกรองความถี่ต่ำ และเราจะถือว่าการแกว่งที่อินพุตขององค์ประกอบที่ไม่เชิงเส้นของ NE เป็นไซน์ จากนั้นสัญญาณเอาต์พุตของ NE คือ:

ที่ไหน โตและ VCคือสัมประสิทธิ์การขยายตัวฟูริเยร์ของฟังก์ชันไม่เชิงเส้น:

หากลักษณะไม่เชิงเส้นสมมาตรและเป็นกลาง แสดงว่าสัมประสิทธิ์การขยายตัวของอนุกรมฟูริเยร์ VC=0 และไม่มีการประสานกันในการขยาย:

การใช้ความสัมพันธ์เหล่านี้ เราแสดงค่าของไซน์และโคไซน์ในรูปของสัญญาณอินพุต

ให้เราแทนที่ความสัมพันธ์เหล่านี้ลงในสมการสำหรับเอาต์พุต NE และพิจารณาเฉพาะฮาร์มอนิกแรกเท่านั้น

เราเขียนสมการนี้ในรูปแบบตัวดำเนินการ:

ค่าสัมประสิทธิ์ A 0 - แอมพลิจูดของการสั่นในตัวเอง q คือสัมประสิทธิ์ของการทำให้เป็นเส้นตรงของฮาร์โมนิกเทียบกับองค์ประกอบไซน์ซึ่งขึ้นอยู่กับแอมพลิจูดของสัญญาณที่อินพุต NE b 1 คือสัมประสิทธิ์ของการทำให้เป็นเส้นตรงฮาร์มอนิกเทียบกับองค์ประกอบโคไซน์ ω 0 คือแอมพลิจูดของการสั่นในตัวเอง

ในกรณีที่ไม่มีองค์ประกอบคงที่ที่อินพุต NE เราได้รับสมการเพื่ออธิบายพฤติกรรมของ NE:

นี่คือสมการเชิงเส้นของฮาร์มอนิกของ NE

NE ที่เป็นเส้นตรงแบบฮาร์โมนิกสามารถแสดงได้ดังนี้:

ในกรณีนี้ เราสามารถหาฟังก์ชันการถ่ายโอนสำหรับ NE ได้:

ในกรณีที่ไม่มีองค์ประกอบคงที่ที่อินพุต

ค่าสัมประสิทธิ์ A 0 - แอมพลิจูดของการสั่นในตัวเอง

q คือสัมประสิทธิ์ของการทำให้เป็นเส้นตรงของฮาร์โมนิกเทียบกับองค์ประกอบไซน์ซึ่งขึ้นอยู่กับแอมพลิจูดของสัญญาณที่อินพุต NE

b 1 คือสัมประสิทธิ์ของการทำให้เป็นเส้นตรงฮาร์มอนิกเทียบกับองค์ประกอบโคไซน์

ω 0 คือแอมพลิจูดของการสั่นในตัวเอง

ส่วนเชิงเส้นของระบบได้รับผลกระทบจากสัญญาณเอาท์พุต NE ซึ่งประกอบด้วยสเปกตรัมความถี่ทั้งหมดของการขยายฟูริเยร์ โดยอาศัยหลักการทับซ้อน เราสามารถสรุปได้ว่าฮาร์มอนิกแต่ละอันทำหน้าที่ในส่วนเชิงเส้นอย่างเป็นอิสระจากอีกส่วนหนึ่ง ดังนั้นการแกว่งเป็นระยะสามารถตั้งค่าได้ที่เอาต์พุตของระบบซึ่งจะมีสเปกตรัมทั้งหมดของความถี่ที่สอดคล้องกับสัญญาณ NE แต่แอมพลิจูดของแต่ละฮาร์มอนิกจะถูกกำหนดโดยค่าสัมประสิทธิ์การแปลงทางด้านขวาสำหรับฮาร์มอนิกที่พิจารณา ( ).

ด้วยการแทนที่การตอบสนองความถี่ของชิ้นส่วนเชิงเส้นตรง คุณสามารถกำหนดอัตราส่วนของการเปลี่ยนแปลงแอมพลิจูดสำหรับแต่ละฮาร์มอนิก และตรวจสอบว่าส่วนเชิงเส้นตรงของ LPF เป็นหรือไม่ (สามารถทิ้งฮาร์มอนิกที่สูงกว่าได้หรือไม่)

หากมีการตั้งค่าความถี่ของการแกว่งตัวเองและทราบค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกของ NE โดยคำนึงถึงฮาร์มอนิกแรกเท่านั้นจากนั้นจึงหมายถึงความถี่ (ความถี่ของฮาร์มอนิกแรก) ถ้าอย่างนั้นคุณสามารถละทิ้งฮาร์โมนิกที่สูงกว่าได้และวิธีนี้ก็เหมาะสม เหล่านั้น. เป็นไปได้ที่จะจำกัดตัวเองให้คำนวณฮาร์มอนิกเพียงอันเดียวที่เอาต์พุต NE จากนั้น สำหรับคุณลักษณะคี่ที่มีค่าเดียว NE จะมี:

สำหรับลักษณะคี่ของฮิสเทรีซิส:

ในกรณีแรก NE จะเทียบเท่ากับการเชื่อมโยงเฉื่อยที่มีคุณสมบัติบางอย่าง - สัมประสิทธิ์สัดส่วนขึ้นอยู่กับแอมพลิจูดหรือความถี่ของสัญญาณที่อินพุต NE

ในกรณีของฮิสทีเรียที่ไม่ใช่เชิงเส้น ลิงค์จะเทียบเท่ากับลิงค์บูสต์ ลักษณะเฉพาะของวิธีการทำให้เป็นเชิงเส้นนี้ทำให้สามารถใช้วิธีความถี่ของทฤษฎีเชิงเส้นในการวิเคราะห์ระบบไม่เชิงเส้นได้

แนวคิดของวิธีการทำให้เป็นเชิงเส้นของฮาร์มอนิกเป็นของ N.M. Krylov และ N.N. Bogolyubov และขึ้นอยู่กับการแทนที่องค์ประกอบที่ไม่เชิงเส้นของระบบด้วยการเชื่อมโยงเชิงเส้นซึ่งพารามิเตอร์ที่กำหนดภายใต้การกระทำอินพุตฮาร์มอนิกจากเงื่อนไขของความเท่าเทียมกันของแอมพลิจูดของฮาร์มอนิกแรกที่เอาต์พุตขององค์ประกอบที่ไม่เชิงเส้นและเทียบเท่า ลิงค์เชิงเส้น วิธีนี้สามารถใช้ได้เมื่อส่วนเชิงเส้นตรงของระบบเป็นตัวกรองความถี่ต่ำผ่าน กล่าวคือ กรองส่วนประกอบฮาร์มอนิกทั้งหมดที่เกิดขึ้นที่เอาต์พุตขององค์ประกอบที่ไม่เป็นเชิงเส้น ยกเว้นฮาร์มอนิกชุดแรก

ค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงของฮาร์โมนิกและการเพิ่มเชิงซ้อนที่เทียบเท่ากันขององค์ประกอบไม่เชิงเส้น ในระบบไม่เชิงเส้น (รูปที่ 2.1) พารามิเตอร์ของส่วนเชิงเส้นและองค์ประกอบไม่เชิงเส้นจะถูกเลือกในลักษณะที่มีการแกว่งเป็นระยะสมมาตรที่มีความถี่ w

หัวใจสำคัญของวิธีการทำให้เป็นเส้นตรงฮาร์มอนิกของความไม่เชิงเส้น (รูปที่ 2.10) อธิบายโดยสมการ

y n = F(x), (2.17)

มีข้อสันนิษฐานว่าการกระทำฮาร์มอนิกที่มีความถี่ w และแอมพลิจูดถูกนำไปใช้กับอินพุตขององค์ประกอบที่ไม่เชิงเส้น เอ, เช่น.

x= เอบาป y โดยที่ y = wt, (2.18)

และมีเพียงฮาร์มอนิกแรกเท่านั้นที่แตกต่างจากสเปกตรัมทั้งหมดของสัญญาณเอาท์พุต

y n 1 = เอ n 1 บาป(y + y n 1), (2.19)

ที่ไหน เอ n 1 - แอมพลิจูดและ y n 1 - การเปลี่ยนเฟส;

ในกรณีนี้ ฮาร์โมนิกที่สูงกว่าจะถูกละทิ้ง และการเชื่อมต่อจะถูกสร้างขึ้นระหว่างฮาร์มอนิกแรกของสัญญาณเอาท์พุตกับเอฟเฟกต์ฮาร์มอนิกอินพุตขององค์ประกอบที่ไม่เชิงเส้น

ข้าว. 2.10. ลักษณะขององค์ประกอบที่ไม่เชิงเส้น

ในกรณีที่ระบบไม่เชิงเส้นไม่ไวต่อฮาร์โมนิกที่สูงกว่า องค์ประกอบที่ไม่เป็นเชิงเส้นสามารถถูกแทนที่ในการประมาณครั้งแรกด้วยองค์ประกอบบางอย่างที่มีอัตราขยายเท่ากัน ซึ่งจะกำหนดฮาร์มอนิกแรกของการแกว่งเป็นระยะที่เอาต์พุต ขึ้นอยู่กับความถี่และแอมพลิจูด ของการแกว่งของไซนัสที่อินพุต

สำหรับองค์ประกอบไม่เชิงเส้นที่มีคุณสมบัติ (2.17) อันเป็นผลมาจากการขยายฟังก์ชันคาบ F(x) เป็นอนุกรมฟูริเยร์ที่มีการสั่นแบบไซน์ที่อินพุต (2.18) เราจะได้นิพจน์สำหรับฮาร์มอนิกแรกของสัญญาณเอาท์พุต

y n 1 = b 1F siny + 1F สบาย ๆ (2.20)

โดยที่ ข 1F , 1F - สัมประสิทธิ์การขยายตัวในอนุกรมฟูริเยร์ซึ่งกำหนดแอมพลิจูดขององค์ประกอบในเฟสและพื้นที่สี่เหลี่ยมจัตุรัสของฮาร์มอนิกแรกตามลำดับซึ่งกำหนดโดยสูตร:

px= เอ w cos y โดยที่ p = d/dt

จากนั้นความสัมพันธ์ระหว่างฮาร์มอนิกแรกของการแกว่งเป็นระยะที่เอาต์พุตขององค์ประกอบไม่เชิงเส้นและการแกว่งของไซน์ที่อินพุตสามารถเขียนได้ดังนี้

y н 1 = x, (2.21)

โดยที่ q = b 1F / เอ, q¢ = ชั้น 1F / เอ.

สมการสุดท้ายเรียกว่า สมการเชิงเส้นฮาร์มอนิกและสัมประสิทธิ์ q และ q¢ - ค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก.

ดังนั้นองค์ประกอบที่ไม่เชิงเส้นเมื่อสัมผัสกับสัญญาณฮาร์มอนิกจะถูกอธิบายโดยสมการ (2.21) ซึ่งเป็นเชิงเส้นจนถึงฮาร์มอนิกที่สูงขึ้น สมการขององค์ประกอบที่ไม่เป็นเชิงเส้นนี้แตกต่างจากสมการของการเชื่อมโยงเชิงเส้นตรงโดยที่ค่าสัมประสิทธิ์ขององค์ประกอบ q และ q เปลี่ยนแปลงตามการเปลี่ยนแปลงของแอมพลิจูด เอและความถี่ w ของการแกว่งที่อินพุต นี่คือความแตกต่างพื้นฐานระหว่างการทำให้เป็นเส้นตรงฮาร์มอนิกและการทำให้เป็นเส้นตรงแบบธรรมดา สัมประสิทธิ์ซึ่งไม่ได้ขึ้นอยู่กับสัญญาณอินพุต แต่จะถูกกำหนดโดยประเภทของคุณลักษณะขององค์ประกอบไม่เชิงเส้นเท่านั้น

สำหรับลักษณะไม่เชิงเส้นประเภทต่างๆ ค่าสัมประสิทธิ์การทำให้เป็นเชิงเส้นของฮาร์มอนิกสรุปไว้ในตาราง ในกรณีทั่วไป ค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก q( เอ, w) และ q¢( เอ, w) ขึ้นอยู่กับแอมพลิจูด เอและความถี่ w ของการแกว่งที่อินพุตขององค์ประกอบไม่เชิงเส้น อย่างไรก็ตาม สำหรับความไม่เชิงเส้นคงที่ สัมประสิทธิ์เหล่านี้ q( เอ) และ q¢( เอ) เป็นเพียงฟังก์ชันของแอมพลิจูด เอสัญญาณฮาร์มอนิกอินพุต และสำหรับความไม่เชิงเส้นที่มีค่าเดียวแบบคงที่ สัมประสิทธิ์ q¢( เอ) = 0.

ภายใต้ Eq. (2.21) กับการแปลง Laplace ภายใต้เงื่อนไขเริ่มต้นเป็นศูนย์ จากนั้นแทนที่ตัวดำเนินการ s ด้วย jw (s = jw) เราได้รับ กำไรเชิงซ้อนเทียบเท่าองค์ประกอบไม่เชิงเส้น

W E (jw, เอ) = q + jq¢ = A อี (w, เอ) e j y e (ว , เอ) , (2.22)

โดยที่โมดูลัสและอาร์กิวเมนต์ของเกนเชิงซ้อนที่เท่ากันนั้นสัมพันธ์กับค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกโดยนิพจน์

เอ อี (ว, เอ) = mod WE (jw, เอ) =

อี อี (w, เอ) = arg W E (jw, A) = arctg

ค่าสัมประสิทธิ์การถ่ายโอนที่ซับซ้อนที่เท่ากันขององค์ประกอบที่ไม่เป็นเชิงเส้นทำให้สามารถกำหนดแอมพลิจูดและการเลื่อนเฟสของฮาร์มอนิกแรก (2.19) ที่เอาต์พุตขององค์ประกอบที่ไม่เป็นเชิงเส้นภายใต้การกระทำของฮาร์มอนิก (2.18) ที่อินพุตนั่นคือ

เอน 1 = เอ'เอ อี (ว, เอ); y n 1 \u003d y E (w, เอ).

ศึกษาระบบเป็นระยะสมมาตรในระบบไม่เชิงเส้นในการศึกษาระบบไม่เชิงเส้นตามวิธีการสร้างเส้นตรงแบบฮาร์มอนิก อย่างแรกเลย ปัญหาเรื่องการมีอยู่และความเสถียรของโหมดคาบนั้นได้รับการแก้ไขแล้ว หากระบอบการปกครองเป็นระยะมีเสถียรภาพแสดงว่ามีการแกว่งตัวในระบบด้วยความถี่ w 0 และแอมพลิจูด เอ 0 .

พิจารณาระบบไม่เชิงเส้น (รูปที่ 2.5) ซึ่งรวมถึงส่วนเชิงเส้นที่มีฟังก์ชันการถ่ายโอน

และองค์ประกอบที่ไม่เป็นเชิงเส้นที่มีค่าเกนเชิงซ้อนเท่ากัน

W E (jw, เอ) = q(w, เอ) + jq¢(w, เอ) = A E (ว, เอ) e j y e (ว , เอ) . (2.24)

เมื่อพิจารณานิพจน์ (2.21) เราสามารถเขียนสมการของระบบไม่เชิงเส้นได้

(A(p) + B(p)´)x = 0 (2.25)

หากเกิดการสั่นในตัวเองในระบบปิดไม่เชิงเส้น

x= เอ 0 บาป w 0 t

ด้วยแอมพลิจูดและความถี่คงที่ สัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกจึงกลายเป็นค่าคงที่ และระบบทั้งหมดหยุดนิ่ง ในการประเมินความเป็นไปได้ของการสั่นในตัวเองในระบบไม่เชิงเส้นโดยใช้วิธีการลิเนียร์ไลเซชันแบบฮาร์โมนิก จำเป็นต้องค้นหาเงื่อนไขสำหรับขอบเขตความเสถียร เช่นเดียวกับที่ทำในการวิเคราะห์ความเสถียรของระบบเชิงเส้น มีวิธีแก้ปัญหาเป็นระยะถ้า เอ = เอ 0 และ w = w 0 สมการคุณลักษณะของระบบเชิงเส้นตรงที่กลมกลืนกัน

A(p) + B(p)´ = 0 (2.26)

มีรากจินตภาพคู่หนึ่ง l i = jw 0 และ l i +1 = -jw 0 ต้องมีการประเมินความเสถียรของโซลูชันเพิ่มเติม

ขึ้นอยู่กับวิธีการแก้สมการลักษณะเฉพาะ วิธีการศึกษาระบบไม่เชิงเส้นจะแตกต่างออกไป

วิธีวิเคราะห์. ในการประเมินความเป็นไปได้ของการสั่นในตัวเองในระบบที่ไม่เชิงเส้น jw ถูกแทนที่เป็นพหุนามลักษณะเชิงเส้นแบบฮาร์โมนิกของระบบแทน p

ด(jw, เอ) = A(jw) + B(jw)´. (2.27)

ผลลัพธ์คือสมการ D(jw, เอ) = 0 ซึ่งสัมประสิทธิ์ขึ้นอยู่กับแอมพลิจูดและความถี่ของระบอบการปกครองแบบออสซิลเลเตอร์ที่สันนิษฐาน การแยกส่วนจริงและส่วนจินตภาพ

เร ดี(jw, เอ) = X(w, เอ);

อิม ดี(jw, เอ) = Y(w, เอ),

เราจะได้สมการ

X(w, เอ) + jY(ว, เอ) = 0. (2.28)

ถ้าค่าจริง เอ 0 และ w 0 นิพจน์ (2.28) เป็นที่พอใจจากนั้นจึงสามารถใช้โหมดการสั่นด้วยตนเองในระบบซึ่งพารามิเตอร์จะคำนวณตามระบบสมการต่อไปนี้:

จากนิพจน์ (2.29) เราสามารถค้นหาการพึ่งพาแอมพลิจูดและความถี่ของการสั่นในตัวเองในพารามิเตอร์ของระบบ ตัวอย่างเช่น บนสัมประสิทธิ์การถ่ายโอน k ของส่วนเชิงเส้นของระบบ ในการทำเช่นนี้ จำเป็นในสมการ (2.29) เพื่อพิจารณาสัมประสิทธิ์การถ่ายโอน k เป็นตัวแปร กล่าวคือ เขียนสมการเหล่านี้ในรูปแบบ:

ตามชาร์ต เอ 0 = f(k), w 0 = f(k) คุณสามารถเลือกค่าสัมประสิทธิ์การถ่ายโอน k ซึ่งแอมพลิจูดและความถี่ของการแกว่งตัวเองที่เป็นไปได้มีค่าที่ยอมรับได้หรือหายไปโดยสมบูรณ์

วิธีความถี่. ตามเกณฑ์ความเสถียรของ Nyquist การสั่นแบบ unamped ในระบบเชิงเส้นตรงเกิดขึ้นเมื่อคุณลักษณะเฟสแอมพลิจูดของระบบ open-loop ผ่านจุดที่มีพิกัด [-1, j0] เงื่อนไขนี้เป็นเงื่อนไขสำหรับการมีอยู่ของการแกว่งตัวในตัวเองในระบบไม่เชิงเส้นเชิงเส้นแบบฮาร์โมนิก กล่าวคือ

W n (jw, เอ) = -1. (2.31)

เนื่องจากส่วนเชิงเส้นและส่วนไม่เชิงเส้นของระบบเชื่อมต่อกันเป็นอนุกรม การตอบสนองความถี่ของระบบไม่เชิงเส้นแบบวงเปิดจึงมีรูปแบบ

W n (jw, เอ) = W lch (jw)´W E (jw, เอ). (2.32)

จากนั้นในกรณีของคุณสมบัติคงที่ขององค์ประกอบที่ไม่เชิงเส้นเงื่อนไข (2.31) จะอยู่ในรูปแบบ

W lch (jw) = - . (2.33)

คำตอบของสมการ (2.33) เกี่ยวกับความถี่และแอมพลิจูดของการสั่นในตัวเองสามารถหาได้แบบกราฟิกเป็นจุดตัดของโฮโดกราฟของการตอบสนองความถี่ของส่วนเชิงเส้นของระบบ W lch (jw) และโฮโดกราฟของ ลักษณะผกผันของส่วนที่ไม่เป็นเชิงเส้น ถ่ายด้วยเครื่องหมายตรงข้าม (รูปที่ 2.11) หากโฮโดกราฟเหล่านี้ไม่ตัดกัน ระบอบการสั่นในตัวเองจะไม่มีอยู่ในระบบที่กำลังศึกษา

ข้าว. 2.11. Hodographs ของส่วนเชิงเส้นและไม่ใช่เชิงเส้นของระบบ

เพื่อความเสถียรของระบบการสั่นในตัวเองด้วยความถี่ w 0 และแอมพลิจูด เอ 0 กำหนดให้จุดบนโฮโดกราฟของส่วนที่ไม่เป็นเชิงเส้น - สอดคล้องกับแอมพลิจูดที่เพิ่มขึ้น เอ 0+ด เอเมื่อเทียบกับค่าที่จุดตัดของโฮโดกราฟ โฮโดกราฟไม่ครอบคลุมถึงการตอบสนองความถี่ของส่วนเชิงเส้นตรงของระบบ และครอบคลุมจุดที่สอดคล้องกับแอมพลิจูดที่ลดลง เอ 0-D เอ.

ในรูป 2.11 ให้ตัวอย่างตำแหน่งของโฮโดกราฟสำหรับกรณีที่เกิดการสั่นในตัวเองที่เสถียรในระบบที่ไม่เป็นเชิงเส้น เนื่องจาก เอ 3 < เอ 0 < เอ 4 .

ศึกษาการตอบสนองความถี่ลอการิทึม.

เมื่อศึกษาระบบไม่เชิงเส้นโดยคุณลักษณะความถี่ลอการิทึม เงื่อนไข (2.31) จะถูกเขียนใหม่แยกกันสำหรับโมดูลัสและอาร์กิวเมนต์ของอัตราขยายเชิงซ้อนที่เท่ากันของระบบไม่เชิงเส้นแบบวงเปิด

mod W lch (jw)W e (jw, เอ) = 1;

หาเรื่อง W lch (jw)W e (jw, เอ) = - (2k+1)p สำหรับ k=0, 1, 2, ...

ด้วยการเปลี่ยนไปใช้แอมพลิจูดลอการิทึมและลักษณะเฟสต่อไป

L ชั่วโมง (w) + L อี (w, เอ) = 0; (2.34)

y lch (w) + y e (w, เอ) = - (2k+1)p สำหรับ k=0, 1, 2, ... (2.35)

เงื่อนไข (2.34) และ (2.35) ทำให้เรากำหนดแอมพลิจูดได้ เอ 0 และความถี่ w 0 ของการแก้ปัญหาสมการคาบ (2.25) ตามลักษณะลอการิทึมของส่วนเชิงเส้นของระบบ L lch (w), y lch (w) และองค์ประกอบไม่เชิงเส้น L e (w, เอ), y e (w, เอ).

การแกว่งตัวเองด้วยความถี่ w 0 และแอมพลิจูด เอ 0 จะมีอยู่ในระบบไม่เชิงเส้นถ้าคำตอบของสมการ (2.25) คงที่ วิธีการโดยประมาณในการศึกษาความเสถียรของสารละลายคาบคือศึกษาพฤติกรรมของระบบที่ความถี่ w = w 0 และค่าแอมพลิจูด เอ =เอ 0+ด เอและ เอ =เอ 0-D เอที่ไหน D เอ> 0 - แอมพลิจูดเพิ่มขึ้นเล็กน้อย เมื่อศึกษาความคงตัวของสารละลายเป็นระยะสำหรับ เอ 0+ด เอและ เอ 0-D เอตามลักษณะลอการิทึม จะใช้เกณฑ์ความเสถียรของ Nyquist

ในระบบไม่เชิงเส้นที่มีคุณสมบัติคงที่ค่าเดียวขององค์ประกอบไม่เชิงเส้น สัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก q¢( เอ) เท่ากับศูนย์ ดังนั้น เท่ากับศูนย์และเฟส shift y e ( เอ) สนับสนุนโดยองค์ประกอบ ในกรณีนี้ แก้สมการของระบบเป็นระยะ

x = 0 (2.36)

มีอยู่หากตรงตามเงื่อนไขต่อไปนี้:

L ชั่วโมง (w) \u003d - L e ( เอ); (2.37)

y lch (w) = - (2k+1)p สำหรับ k=0, 1, 2, ... (2.38)

สมการ (2.38) ช่วยให้เราสามารถกำหนดความถี่ w \u003d w 0 ของคำตอบเป็นระยะและสมการ (2.37) - แอมพลิจูดของมัน เอ =เอ 0 .

ด้วยส่วนเชิงเส้นที่ค่อนข้างง่าย จึงสามารถหาคำตอบของสมการเหล่านี้ได้ในเชิงวิเคราะห์ อย่างไรก็ตาม ในกรณีส่วนใหญ่ แนะนำให้แก้ปัญหาแบบกราฟิก (รูปที่ 2.12)

เมื่อศึกษาความเสถียรของคำตอบของสมการเป็นระยะ (2.36) เช่น เมื่อพิจารณาการมีอยู่ของการแกว่งตัวเองในระบบไม่เชิงเส้นที่มีลักษณะคงที่ไม่เชิงเส้นที่มีค่าเดียว เกณฑ์ Nyquist: คำตอบเป็นระยะด้วยความถี่ w = w 0 และแอมพลิจูด เอ =เอ 0 จะคงที่หากความถี่เปลี่ยนจากศูนย์เป็นอนันต์และแอมพลิจูดเพิ่มขึ้นเป็นบวก D เอ> 0 ความแตกต่างระหว่างจำนวนการเปลี่ยนเชิงบวก (จากบนลงล่าง) และเชิงลบ (จากล่างขึ้นบน) ของลักษณะเฟสของส่วนเชิงเส้นของระบบ y lch (w) ผ่านเส้น -p เป็นศูนย์ในความถี่ ช่วง โดยที่ L lch (w)³-L e (w 0 , เอ 0+ด เอ) และไม่เท่ากับศูนย์ในช่วงความถี่ โดยที่ L h (w)³-L e (w 0 เอ 0-D เอ).

ในรูป 2.12 แสดงตัวอย่างการกำหนดคำตอบเป็นระยะในระบบไม่เชิงเส้นพร้อมข้อจำกัด ในระบบดังกล่าวมีวิธีแก้ปัญหาเป็นระยะสามช่วงที่มีความถี่ w 01 , w 02 และ w 03 กำหนดที่จุดตัดของลักษณะเฟส y lch (w) กับเส้น -180 0 . แอมพลิจูดของสารละลายเป็นระยะ เอ 01 , เอ 02 และ เอ 03 ถูกกำหนดจากเงื่อนไข (2.37) โดยลักษณะแอมพลิจูดลอการิทึมขององค์ประกอบไม่เชิงเส้น -L e (w 01 , เอ), -L e (w 02, เอ) และ -L e (w 03, เอ).

ข้าว. 2.12. แอมพลิจูดลอการิทึมและลักษณะเฟส

จากสามโซลูชันที่กำหนดไว้ในรูปที่ 2.12 สองตัวเสถียร โซลูชันที่มีความถี่ w = w 01 และแอมพลิจูด เอ =เอ 01 มีเสถียรภาพเนื่องจากในช่วงความถี่ 1 โดยที่ L lch (w)³-L e (w 01, เอ 01+ด เอ) ลักษณะเฟส y lch (w) ไม่ข้ามเส้น -180 0 แต่ในช่วงความถี่ 2 โดยที่ L lch (w)³-L e (w 01, เอ 01-D เอ) ลักษณะเฟส y lch (w) เมื่อข้ามเส้น -180 0 . โซลูชันที่มีความถี่ w = w 02 และ amplitude เอ =เอ 02 ไม่เสถียรเนื่องจากอยู่ในช่วงความถี่ที่ L h (w)³-L e (w 02, เอ 02+D เอ) ลักษณะเฟส y lch (w) เมื่อข้ามเส้น -180 0 . สารละลายคาบความถี่สูงที่มีความถี่ w = w 03 และแอมพลิจูด เอ =เอ 03 มีเสถียรภาพเพราะในช่วงความถี่โดยที่ L ชั่วโมง (w)³-L e (w 03, เอ 03+ด เอ) มีการเปลี่ยนลักษณะเฟสเป็นบวกและลบหนึ่งครั้ง y lch (w) ผ่านเส้น -180 0 และในช่วงความถี่ที่ L lch (w)³-L e (w 03, เอ 03-D เอ) มีการเปลี่ยนลักษณะเฟสเป็นบวกและลบสองครั้ง y lch (w) ผ่านเส้น -180 0 .

ในระบบที่พิจารณาแล้ว โดยมีการรบกวนเล็กน้อย การสั่นในตัวเองด้วยความถี่สูงด้วยความถี่ w 03 และแอมพลิจูด เอ 03 และสำหรับการก่อกวนขนาดใหญ่ - การสั่นในตัวเองด้วยความถี่ต่ำด้วยความถี่ w 01 และแอมพลิจูด เอ 01 .

ตัวอย่าง.ตรวจสอบโหมดการสั่นในตัวเองในระบบที่ไม่เป็นเชิงเส้น ซึ่งส่วนเชิงเส้นซึ่งมีฟังก์ชันการถ่ายโอนดังต่อไปนี้

โดยที่ k=200 s -1 ; T 1 =1.5 วิ; T 2 \u003d 0.015 วิ

และในฐานะองค์ประกอบที่ไม่เป็นเชิงเส้นจะใช้รีเลย์ที่มีโซนตาย (รูปที่ 2.4, b) ที่ c=10 V, b=2 V.

สารละลาย ตามตารางสำหรับรีเลย์ที่มีโซนตายเราพบค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก:

ที่ เอ³ b, q¢( เอ) = 0.

เมื่อสร้างคุณสมบัติขององค์ประกอบที่ไม่เชิงเส้น ขอแนะนำให้ใช้ค่าสัมพัทธ์ของแอมพลิจูดของเอฟเฟกต์ฮาร์มอนิกอินพุต m = เอ/ข. ให้เราเขียนนิพจน์สำหรับค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกใหม่ในรูปแบบ

ค่าสัมประสิทธิ์การส่งของรีเลย์อยู่ที่ไหน

แอมพลิจูดสัมพัทธ์

ค่าสัมประสิทธิ์การถ่ายโอนรีเลย์ k n เกี่ยวข้องกับส่วนเชิงเส้นของระบบและเราได้รับค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกที่ทำให้เป็นมาตรฐาน

และลักษณะแอมพลิจูดลอการิทึมที่ทำให้เป็นมาตรฐานขององค์ประกอบรีเลย์ที่มีเครื่องหมายตรงข้าม

ถ้า m ® 1 แล้ว -L e (m) ® ¥; และเมื่อ m >> 1 -L e (m) = 20 lg m. ดังนั้น เส้นกำกับของคุณลักษณะแอมพลิจูดลอการิทึมปกติที่มีเครื่องหมายตรงข้ามคือเส้นตรงแนวตั้งและเส้นตรงที่มีความชัน +20 เดซิเบล/เดก ซึ่งผ่านจุดที่มีพิกัด L = 0, m = 1 (รูปที่ 2.13).

ข้าว. 2.13. การกำหนดวิธีแก้ปัญหาเป็นระยะในระบบรีเลย์

กับเดดโซน

เอ 0 = b´m 1 = = 58 V.

เพื่อแก้ปัญหาการมีอยู่ของการแกว่งตัวเองตามลักษณะแอมพลิจูดลอการิทึมปกติที่มีเครื่องหมายตรงข้ามขององค์ประกอบไม่เชิงเส้นและฟังก์ชันการถ่ายโอนของส่วนเชิงเส้นของระบบ

ในรูป 2.13 วาดลักษณะลอการิทึมของ L ch (w), -L e (m) และ y ch (w)

ความถี่ของการแก้ปัญหาเป็นระยะ w 0 = 4.3 s -1 ถูกกำหนดที่จุดตัดของลักษณะเฟส y lch (w) และเส้น -180 0 . แอมพลิจูดของสารละลายคาบ m 1 = 29 และ m 2 = 1.08 พบได้ตามลักษณะ L ชั่วโมง (w) และ -L e (m) สารละลายคาบที่มีแอมพลิจูดน้อย ม. 2 จะไม่เสถียร ในขณะที่สารละลายคาบที่มีแอมพลิจูดมาก ม. 1 จะเสถียร

ดังนั้นในระบบรีเลย์ที่ศึกษาจึงมีโหมดการสั่นในตัวเองด้วยความถี่ w 0 = 4.3 s -1 และแอมพลิจูด เอ 0 = b´m 1 = = 58 V.

กระทรวงศึกษาธิการและวิทยาศาสตร์แห่งสหพันธรัฐรัสเซีย

มหาวิทยาลัยเทคนิคแห่งรัฐ Saratov

Balakov สถาบันวิศวกรรม เทคโนโลยี และการจัดการ

วิธีการลิเนียร์ไลเซชันแบบฮาร์มอนิก

แนวทางการทำงานในห้องปฏิบัติการในหลักสูตร "ทฤษฎี ระบบควบคุมอัตโนมัติ» สำหรับนักศึกษาพิเศษ 210100

ที่ได้รับการอนุมัติ

กองบรรณาธิการและสำนักพิมพ์

สถาบันเทคโนโลยีบาลาโกโว,

เทคโนโลยีและการจัดการ

บาลาโคโว 2004

วัตถุประสงค์ของงาน: การศึกษาระบบไม่เชิงเส้นโดยใช้วิธีการเชิงเส้นฮาร์มอนิก (สมดุลฮาร์มอนิก) การหาค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกสำหรับลิงก์ไม่เชิงเส้นต่างๆ การได้รับทักษะในการค้นหาพารามิเตอร์ของการแกว่งแบบสมมาตรของแอมพลิจูดและความถี่คงที่ (การสั่นในตัวเอง) โดยใช้วิธีการเกี่ยวกับพีชคณิต วิธีความถี่ ตลอดจนการใช้เกณฑ์ของมิคาอิลอฟ

ข้อมูลพื้นฐาน

วิธีการเชิงเส้นฮาร์มอนิกหมายถึงวิธีการโดยประมาณสำหรับการศึกษาระบบไม่เชิงเส้น ทำให้สามารถประเมินความเสถียรของระบบไม่เชิงเส้นได้ค่อนข้างง่ายและด้วยความแม่นยำที่ยอมรับได้ และเพื่อกำหนดความถี่และแอมพลิจูดของการแกว่งที่เกิดขึ้นในระบบ

สันนิษฐานว่า ACS ที่ไม่เชิงเส้นที่ตรวจสอบแล้วสามารถแสดงได้ในรูปแบบต่อไปนี้

ยิ่งกว่านั้น ส่วนที่ไม่เป็นเชิงเส้นต้องมีหนึ่งส่วนไม่เชิงเส้น

. (1)

ความไม่เป็นเชิงเส้นนี้สามารถเป็นได้ทั้งแบบต่อเนื่องหรือแบบรีเลย์, ชัดเจนหรือแบบฮิสทีเรีย

ฟังก์ชันหรือสัญญาณใดๆ สามารถขยายออกเป็นอนุกรมตามระบบที่เป็นอิสระเชิงเส้น ในบางกรณี ฟังก์ชันออร์โธนอร์มอล อนุกรมฟูริเยร์สามารถใช้เป็นอนุกรมมุมฉากได้

ให้เราขยายสัญญาณเอาท์พุตของส่วนไม่เชิงเส้นของระบบเป็นอนุกรมฟูริเยร์

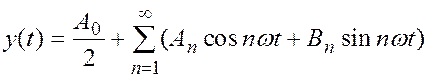, (2)

นี่คือสัมประสิทธิ์ฟูริเยร์

,

,

. (3)

ดังนั้นสัญญาณตาม (2) สามารถแสดงเป็นผลรวมของฮาร์มอนิกที่ไม่มีที่สิ้นสุดด้วยความถี่ที่เพิ่มขึ้น เป็นต้น สัญญาณนี้ถูกป้อนเข้าสู่ส่วนเชิงเส้นของระบบไม่เชิงเส้น

ให้เราแสดงถึงฟังก์ชันการถ่ายโอนของส่วนเชิงเส้น

, (4)

และดีกรีของพหุนามตัวเศษต้องน้อยกว่าดีกรีของพหุนามตัวส่วน ในกรณีนี้การตอบสนองความถี่ของส่วนเชิงเส้นจะมีรูปแบบ

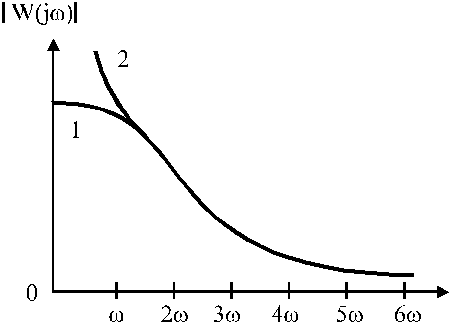
โดยที่ 1 - ไม่มีเสา 2 - มีเสาหรือเสา

สำหรับการตอบสนองความถี่ก็ยุติธรรมที่จะเขียน

ดังนั้น ส่วนเชิงเส้นของระบบไม่เชิงเส้นจึงเป็นตัวกรองความถี่สูง ในกรณีนี้ ส่วนที่เป็นเส้นตรงจะส่งผ่านเฉพาะความถี่ต่ำโดยไม่มีการลดทอน ขณะที่ความถี่สูงจะลดลงอย่างมากเมื่อความถี่เพิ่มขึ้น

วิธีการทำให้เป็นเชิงเส้นของฮาร์มอนิกถือว่าส่วนเชิงเส้นของระบบจะส่งผ่านเฉพาะส่วนประกอบ DC ของสัญญาณและฮาร์มอนิกแรกเท่านั้น จากนั้นสัญญาณที่เอาต์พุตของส่วนเชิงเส้นจะมีลักษณะดังนี้

สัญญาณนี้ผ่านลูปปิดทั้งหมดของระบบ รูปที่ 1 และที่เอาต์พุตขององค์ประกอบที่ไม่เป็นเชิงเส้นโดยไม่คำนึงถึงฮาร์มอนิกที่สูงขึ้นตาม (2) เรามี

. (7)

ในการศึกษาระบบไม่เชิงเส้นโดยใช้วิธีการทำให้เป็นเส้นตรงแบบฮาร์โมนิก กรณีของการแกว่งแบบสมมาตรและไม่สมมาตรเป็นไปได้ ให้เราพิจารณากรณีของการแกว่งแบบสมมาตร ที่นี่และ.

เราแนะนำสัญกรณ์ต่อไปนี้

,

.

แทนที่พวกเขาใน (7) เราได้รับ . (แปด)

โดยคำนึงถึงความจริงที่ว่า

,

, ที่ไหน ,

. (9)

ตาม (3) และ (8) ที่

,

. (10)

นิพจน์ (9) คือการทำให้เป็นเส้นตรงแบบฮาร์มอนิกของความไม่เชิงเส้น กำหนดความสัมพันธ์เชิงเส้นระหว่างตัวแปรอินพุตและตัวแปรเอาต์พุตที่ ปริมาณและเรียกว่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก

ควรสังเกตว่าสมการ (9) เป็นเส้นตรงสำหรับค่าเฉพาะและ (แอมพลิจูดและความถี่ของการสั่นฮาร์มอนิกในระบบ) แต่โดยทั่วไปจะคงคุณสมบัติไม่เชิงเส้นไว้เนื่องจากค่าสัมประสิทธิ์ต่างกันสำหรับค่าต่างๆ และ . คุณลักษณะนี้ช่วยให้เราสามารถสำรวจคุณสมบัติของระบบไม่เชิงเส้นโดยใช้วิธีการทำให้เป็นเส้นตรงแบบฮาร์มอนิก [Popov E.P. ]

ในกรณีของการแกว่งแบบไม่สมมาตร การทำให้เป็นเส้นตรงแบบฮาร์มอนิกของความไม่เชิงเส้นนำไปสู่สมการเชิงเส้น

,

,

. (12)

เช่นเดียวกับสมการ (9) สมการเชิงเส้นตรง (11) ยังคงคุณสมบัติขององค์ประกอบไม่เชิงเส้น เนื่องจากสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก , เช่นเดียวกับองค์ประกอบคงที่ขึ้นอยู่กับทั้งการกระจัดและแอมพลิจูดของการสั่นฮาร์มอนิก .

สมการ (9) และ (11) ยอมให้ได้รับฟังก์ชันการถ่ายโอนขององค์ประกอบที่ไม่เชิงเส้นเชิงเส้นแบบฮาร์โมนิก ดังนั้นสำหรับการสั่นแบบสมมาตร

ดังที่ได้กล่าวไปแล้ว ในลักษณะไม่เชิงเส้นและโดยเฉพาะอย่างยิ่ง ACP แบบถ่ายทอด มักมีการสังเกตพบบ่อย ความผันผวนเป็นระยะที่เสถียรแอมพลิจูดและความถี่คงที่ที่เรียกว่า การสั่นไหวในตัวเอง. นอกจากนี้ การสั่นในตัวเองสามารถคงอยู่ได้แม้จะมีการเปลี่ยนแปลงที่สำคัญในพารามิเตอร์ระบบ จากการปฏิบัติแสดงให้เห็นว่าในหลายกรณีความผันผวนของค่าควบคุม (รูปที่ 3) ใกล้เคียงกับฮาร์มอนิก

ความใกล้ชิดของการสั่นในตัวเองกับฮาร์มอนิกทำให้สามารถใช้วิธีการเชิงเส้นฮาร์มอนิกเพื่อกำหนดพารามิเตอร์ - แอมพลิจูด A และความถี่ w 0 . วิธีการนี้ขึ้นอยู่กับสมมติฐานที่ว่าส่วนเชิงเส้นของระบบเป็นตัวกรองความถี่ต่ำ (สมมติฐานตัวกรอง) ให้เราพิจารณาเงื่อนไขที่การสั่นในตัวเองในระบบสามารถใกล้เคียงกับฮาร์มอนิกได้ เราจำกัดตัวเองให้อยู่ในระบบดังในรูปที่ 3 สามารถลดลงเป็นการเชื่อมต่อแบบอนุกรมขององค์ประกอบที่ไม่เป็นเชิงเส้นและส่วนเชิงเส้น เราคิดว่าสัญญาณอ้างอิงเป็นค่าคงที่ เพื่อความง่าย เราจะเอามันมาเท่ากับศูนย์ และสัญญาณผิดพลาด (รูปที่ 3) เป็นฮาร์มอนิก:

สัญญาณเอาท์พุตของอิลิเมนต์ที่ไม่เป็นเชิงเส้น เช่นเดียวกับสัญญาณคาบใดๆ - ในรูปที่ 3 เหล่านี้คือการสั่นแบบสี่เหลี่ยม - สามารถแสดงเป็นผลรวมของฮาร์โมนิกของอนุกรมฟูริเยร์

สมมติว่าส่วนเชิงเส้นของระบบเป็นตัวกรองความถี่ต่ำ (รูปที่ 4) และส่งผ่านเฉพาะฮาร์มอนิกแรกที่มีความถี่ w 0 . วินาทีที่มีความถี่ 2w 0 และฮาร์มอนิกที่สูงกว่าจะถูกกรองโดยส่วนเชิงเส้น ในกรณีนี้ บน เอาต์พุตเชิงเส้น ชิ้นส่วนจะมีอยู่จริงเท่านั้น ฮาร์โมนิกแรก และอิทธิพลของฮาร์โมนิกที่สูงขึ้นสามารถละเลยได้

ดังนั้น หากส่วนเชิงเส้นของระบบเป็นตัวกรองความถี่ต่ำผ่าน และความถี่การสั่นในตัวเอง w 0 เป็นไปตามเงื่อนไข

, (4)

สมมติฐานที่ว่าส่วนเชิงเส้นของระบบเป็นตัวกรองความถี่ต่ำเรียกว่า กรองสมมติฐาน . สมมติฐานตัวกรองเป็นที่พอใจเสมอหากความแตกต่างระหว่างองศาของพหุนามของตัวส่วนและตัวเศษของฟังก์ชันการถ่ายโอนของส่วนเชิงเส้น

อย่างน้อยสอง

เงื่อนไข (6) เป็นที่พอใจสำหรับระบบจริงจำนวนมาก ตัวอย่างคือลิงค์ aperiodic ของลำดับที่สองและการบูรณาการที่แท้จริง

เมื่อศึกษาการสั่นในตัวเองที่ใกล้เคียงกับฮาร์มอนิก จะพิจารณาเฉพาะฮาร์มอนิกแรกของการแกว่งตามคาบที่เอาต์พุตขององค์ประกอบที่ไม่เป็นเชิงเส้น เนื่องจากฮาร์มอนิกที่สูงกว่าจะถูกกรองออกโดยส่วนเชิงเส้นอยู่แล้ว ในโหมดการสั่นในตัวเอง การทำให้เป็นเส้นตรงฮาร์มอนิก องค์ประกอบที่ไม่เป็นเชิงเส้น องค์ประกอบที่ไม่เป็นเชิงเส้นจะถูกแทนที่ด้วยองค์ประกอบเชิงเส้นที่เทียบเท่ากับ กำไรที่ซับซ้อน (ฟังก์ชันอธิบาย) ขึ้นอยู่กับแอมพลิจูดของสัญญาณฮาร์มอนิกอินพุต:

โดยที่ และ คือ ส่วนจริงและจินตภาพของ ,

- การโต้เถียง,

- โมดูล.

ในกรณีทั่วไป ขึ้นอยู่กับทั้งแอมพลิจูดและความถี่ของการสั่นในตัวเองและส่วนประกอบคงที่ การเพิ่มองค์ประกอบที่ไม่เป็นเชิงเส้นที่ซับซ้อนทางกายภาพ โดยทั่วไปเรียกว่า ค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิก , มี การเพิ่มเชิงซ้อนขององค์ประกอบไม่เชิงเส้นในฮาร์มอนิกแรก. โมดูลัสสัมประสิทธิ์การเชิงเส้นฮาร์มอนิก

ตัวเลขเท่ากับอัตราส่วนของแอมพลิจูดของฮาร์มอนิกแรกที่เอาต์พุตขององค์ประกอบที่ไม่เชิงเส้นต่อแอมพลิจูดของสัญญาณฮาร์มอนิกอินพุต

การโต้เถียง

แสดงลักษณะการเปลี่ยนเฟสระหว่างฮาร์มอนิกแรกของออสซิลเลชันเอาต์พุตและสัญญาณฮาร์มอนิกอินพุต สำหรับความไม่เชิงเส้นที่มีค่าเดียว เช่น ในรูปที่ 2a และ 2b นิพจน์จริงและ

สำหรับความไม่เชิงเส้นที่คลุมเครือ, รูปที่ 2, c, 2, d, ถูกกำหนดโดยสูตร

โดยที่ S คือพื้นที่ของวงฮิสเทรีซิส พื้นที่ S จะถูกถ่ายด้วยเครื่องหมายบวก ถ้าลูปฮิสเทรีซิสถูกข้ามไปในทิศทางบวก (รูปที่ 2c) และด้วยเครื่องหมายลบ (รูปที่ 2d)

ในกรณีทั่วไปและคำนวณโดยสูตร

โดยที่ เป็นฟังก์ชันไม่เชิงเส้น (ลักษณะขององค์ประกอบที่ไม่เชิงเส้น)

จากที่กล่าวมาข้างต้น ในการศึกษาการสั่นในตัวเองใกล้กับฮาร์มอนิก ASR แบบไม่เชิงเส้น (รูปที่ 3) จะถูกแทนที่ด้วยค่าที่เทียบเท่ากันด้วยค่าสัมประสิทธิ์การทำให้เป็นเชิงเส้นของฮาร์มอนิกแทนที่จะเป็นองค์ประกอบที่ไม่เป็นเชิงเส้น (รูปที่ 5) สัญญาณเอาท์พุตขององค์ประกอบที่ไม่เป็นเชิงเส้นในรูปที่ 5 ถูกทำเครื่องหมายเป็น มันคือ

เน้นว่าองค์ประกอบที่ไม่เชิงเส้นสร้างเท่านั้น

ฮาร์โมนิกแรกของการสั่นสะเทือน สูตรสำหรับสัมประสิทธิ์การทำให้เป็นเชิงเส้นของฮาร์มอนิกสำหรับความไม่เชิงเส้นทั่วไปมีอยู่ในเอกสารประกอบ เช่น ใน ตารางในภาคผนวก ข แสดงคุณลักษณะขององค์ประกอบการถ่ายทอดที่ศึกษา สูตรสำหรับ และภาพสามมิติ นอกจากนี้ยังมีสูตรและโฮโดกราฟสำหรับค่าสัมประสิทธิ์ส่วนกลับของการทำให้เป็นเส้นตรงฮาร์มอนิกซึ่งกำหนดโดยนิพจน์

ส่วนจริงและจินตภาพของ . โฮโดกราฟและถูกพล็อตในพิกัด และ และ ตามลำดับ

ตอนนี้ให้เราเขียนเงื่อนไขสำหรับการมีอยู่ของการแกว่งตัวในตัวเอง ระบบในรูป 5 เทียบเท่ากับเส้นตรง ในระบบเชิงเส้นตรง มีการสั่นแบบไม่แดมป์หากอยู่บนขอบเขตของความเสถียร ให้เราใช้เงื่อนไขของขอบเขตความมั่นคงตามเกณฑ์ Nyquist: ในรูป 6a – จุดตัดสองจุด ซึ่งบ่งชี้ว่ามีวงจรจำกัดสองรอบ

วิธีการลิเนียร์ไลเซชันแบบฮาร์โมนิกช่วยให้เราสามารถศึกษาความเสถียรและความถูกต้องของระบบไม่เชิงเส้นที่มีความแม่นยำเพียงพอสำหรับการปฏิบัติ โดยใช้วิธีการที่พัฒนาขึ้นสำหรับระบบเชิงเส้นตรง วิธีนี้ทำให้สามารถระบุการมีอยู่ของการสั่นในตัวเองได้ เช่นเดียวกับความถี่และแอมพลิจูด

ระบบที่ไม่เป็นเชิงเส้นจะแสดงเป็นการรวมกันของส่วนเชิงเส้นและส่วนที่ไม่ใช่เชิงเส้น (รูปที่ 5)

ข้าว. 5 ไดอะแกรมของระบบไม่เชิงเส้น

สัญญาณเอาท์พุตของส่วนไม่เชิงเส้นของระบบโดยทั่วไปถูกกำหนดโดยนิพจน์

แสดงว่าเป็นฟังก์ชันการถ่ายโอนของส่วนเชิงเส้น ระบบสมการอยู่ในรูป

ให้เราหาเงื่อนไขภายใต้การสั่นของรูปแบบที่เกิดขึ้นที่เอาต์พุตของส่วนเชิงเส้นของระบบ

ในกรณีนี้สัญญาณ ญ(ท)ส่วนที่ไม่เป็นเชิงเส้นจะเป็นฟังก์ชันคาบ แต่แตกต่างจากไซนัสอยด์ ฟังก์ชันนี้สามารถขยายเป็นอนุกรมฟูริเยร์ได้

ในนิพจน์นี้ เอ ผมและ ข ผม- สัมประสิทธิ์ฟูริเยร์ สำหรับความไม่เชิงเส้นสมมาตร F 0 =0.

เงื่อนไขหลักที่วิธีการกำหนดในส่วนเชิงเส้นของระบบคือเงื่อนไขของตัวกรองความถี่ต่ำผ่าน เชื่อกันว่าส่วนเชิงเส้นส่งผ่านเฉพาะฮาร์มอนิกของการสั่นครั้งแรกเท่านั้น สมมติฐานนี้ทำให้เราพิจารณาฮาร์โมนิกที่สูงกว่าใน (7.19) ที่ไม่มีนัยสำคัญและจำกัดตัวเราให้พิจารณาเฉพาะฮาร์มอนิกแรกของสัญญาณเท่านั้น y(t).

จากนั้นนิพจน์ (7.20) สามารถเขียนใหม่เป็น

สมการแรกของระบบ (7.17) อยู่ในรูปแบบ

ในนิพจน์นี้

ผลของการแทนที่ความไม่เชิงเส้น ฉ(x, sx)การแสดงออก

และเรียกว่าการทำให้เป็นเส้นตรงแบบฮาร์มอนิก ปริมาณ qและ q 1 เรียกว่าสัมประสิทธิ์การทำให้เป็นเชิงเส้นของฮาร์มอนิกหรือสัมประสิทธิ์ฮาร์มอนิก สำหรับความไม่เชิงเส้นที่มีค่าเดียว โดยปกติ q 1 =0 . สูตรสำหรับสัมประสิทธิ์ฮาร์มอนิกที่สอดคล้องกับความไม่เชิงเส้นทั่วไปมีอยู่ในภาคผนวก

ความแตกต่างพื้นฐานระหว่างการทำให้เป็นเส้นตรงแบบฮาร์มอนิกและการทำให้เป็นเส้นตรงแบบธรรมดาคือ เมื่อใช้การทำให้เป็นเส้นตรงแบบธรรมดา คุณลักษณะไม่เชิงเส้นจะถูกแทนที่ด้วยเส้นตรงที่มีความชันคงที่ที่แน่นอน และด้วยการทำให้เป็นเส้นตรงแบบฮาร์มอนิกโดยเส้นตรง ความชันขึ้นอยู่กับแอมพลิจูดของ สัญญาณอินพุตขององค์ประกอบไม่เชิงเส้น

พิจารณาวิธีการกำหนดแอมพลิจูดและความถี่ของการสั่นในตัวเอง

หนึ่ง). ในสมการคุณลักษณะของระบบที่ได้จาก (7.22) เราทำการเปลี่ยนแปลง s=jและรับ

2). จากนิพจน์ผลลัพธ์ เราเลือกส่วนจริงและส่วนจินตภาพและจัดพวกมันให้เป็นศูนย์ ซึ่งตามเกณฑ์ของมิคาอิลอฟ สอดคล้องกับระบบที่อยู่บนขอบเขตความเสถียรของการสั่น

• 3) การแก้ปัญหาของระบบนี้ให้ความถี่และค่าของสัมประสิทธิ์ฮาร์มอนิก หากค่าเหล่านี้เป็นค่าจริงและเป็นบวก แสดงว่าระบบมีวงจรจำกัด ค่าของสัมประสิทธิ์ฮาร์มอนิกสามารถใช้กำหนดแอมพลิจูดของรอบจำกัดได้
• 4). สัญญาณทั่วไปของความเสถียรของวงจรจำกัด กล่าวคือ การมีอยู่ของการสั่นในตัวเองคือความเท่าเทียมกันเป็นศูนย์ของตัวกำหนด Hurwitz สุดท้ายสำหรับค่าที่ได้รับของแอมพลิจูดและความถี่ของรอบขีด จำกัด มักจะสะดวกกว่าที่จะใช้เงื่อนไขความเสถียรของวงจรจำกัดตามเกณฑ์ความเสถียรของ Mikhailov

หากเกิดความไม่เท่าเทียมกันนี้ แสดงว่ารอบการจำกัดจะคงที่และมีการสั่นในตัวเองในระบบด้วยแอมพลิจูดและความถี่ที่กำหนดไว้ข้างต้น ดัชนี ”*” หมายความว่าอนุพันธ์คำนวณด้วยค่าสัมประสิทธิ์ฮาร์มอนิก แอมพลิจูด และความถี่ที่ทราบอยู่แล้ว

ตัวอย่าง. สมมุติว่าในระบบรักษาเสถียรภาพมุมพิทช์ของเครื่องบินที่พิจารณาข้างต้นแล้ว เฟืองบังคับเลี้ยวเป็นแบบไม่เป็นเส้นตรงและแผนภาพของบล็อกมีรูปแบบดังแสดงในรูปที่ 7.6.

รูปที่ 6 ไดอะแกรมของไดรฟ์พวงมาลัยแบบไม่เป็นเชิงเส้น

ให้เราตั้งค่าพารามิเตอร์ต่อไปนี้ของความไม่เชิงเส้นของลักษณะความเร็วของเฟืองบังคับเลี้ยว: b = 0.12, k 1 =tg =c/b = 6.7.ค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกของความไม่เชิงเส้นนี้ถูกกำหนดโดยนิพจน์

การเปลี่ยนคุณสมบัติไม่เชิงเส้นในวงจรด้วยค่าสัมประสิทธิ์ฮาร์มอนิกเราได้รับฟังก์ชั่นการถ่ายโอนของเฟืองพวงมาลัย

เราแทนที่ฟังก์ชันการถ่ายโอนนี้ลงในแผนภาพบล็อกของระบบรักษาเสถียรภาพมุมพิทช์และกำหนดฟังก์ชันการถ่ายโอนของระบบปิด

ในสมการคุณลักษณะของระบบปิด เราทำการเปลี่ยนแปลง ส = เจและเลือกส่วนจริงและส่วนจินตภาพ

จากสมการที่สองของระบบ เราได้นิพจน์สำหรับความถี่: และแทนที่มันเป็นสมการแรก หลังจากการแปลง เราได้รับ

แทนที่นิพจน์ที่กำหนดไว้ก่อนหน้านี้สำหรับสัมประสิทธิ์ของสมการคุณลักษณะเราสามารถหาสมการกำลังสองเทียบกับค่าสัมประสิทธิ์ฮาร์มอนิกซึ่งเราพบว่า

จากค่าเหล่านี้คุณสามารถคำนวณค่าสัมประสิทธิ์ทั้งหมดของสมการคุณลักษณะและกำหนดความถี่ที่สอดคล้องกับแต่ละค่าได้สองกรณี q(A).เราได้รับ:

ค่าสัมประสิทธิ์ฮาร์มอนิกทั้งสองและความถี่ที่สอดคล้องกันนั้นเป็นค่าจริงและเป็นค่าบวก ดังนั้นจึงมีวงจรจำกัดสองรอบในระบบ ค่าของแอมพลิจูดรอบขีด จำกัด ถูกกำหนดเป็นตัวเลขโดยการเลือกค่าดังกล่าวซึ่งสูตรสำหรับสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกให้ค่าเท่ากับค่าที่คำนวณก่อนหน้านี้ ในกรณีที่อยู่ระหว่างการพิจารณาเราได้รับ

ตอนนี้ ให้เราประเมินความเสถียรของรอบขีดจำกัด เราใช้ความไม่เท่าเทียมกันที่ได้รับจากเกณฑ์ Mikhailov ซึ่งเรากำหนด

อนุพันธ์ของค่าสัมประสิทธิ์การทำให้เป็นเส้นตรงฮาร์มอนิกที่รวมอยู่ในนิพจน์ที่ได้รับคำนวณโดยสูตร

การคำนวณโดยใช้สูตรข้างต้นแสดงว่าลิมิตรอบแรกไม่เสถียรและเกิดขึ้นเมื่อ (0) 0.1166(6.7 0 ). หากค่าเบี่ยงเบนเริ่มต้นน้อยกว่าค่าที่ระบุ กระบวนการที่อินพุตขององค์ประกอบไม่เชิงเส้นจะสลายตัว (รูปที่ 7. 7) และระบบจะเสถียร

หากค่าเริ่มต้นของมุมพิทช์มากกว่าค่าที่ระบุ กระบวนการก็จะมาบรรจบกันเป็นรอบขีดจำกัดที่สอง ซึ่งคงที่ และด้วยเหตุนี้ การสั่นในตัวเองจึงเกิดขึ้นในระบบ (รูปที่ 8)

ข้าว. แปด

โดยการสร้างแบบจำลอง จะกำหนดว่าพื้นที่ดึงดูดของรอบขีดจำกัดที่เสถียรนั้นอยู่ภายในโดยประมาณ (0) 0.1167 - 1.4 (6.71 0 - 80.2 0 ).