Linearizarea armonică a elementelor neliniare. Această metodă este utilizată pentru a studia sistemele neliniare cu o parte liniară deasupra ordinului al treilea. În majoritatea sistemelor, procesul tranzitoriu este o oscilație amortizată, prin urmare, la intrarea unui element neliniar de-a lungul părere(GOS) un semnal periodic este transmis cu o amplitudine care se schimbă lent și, în prezența unui semnal de intrare, împreună cu o componentă constantă.

Vom presupune că la intrarea unui element neliniar pentru o anumită perioadă inițială mică de timp, amplitudinea și frecvența nu se modifică sau corespund amplitudinii și frecvenței auto-oscilațiilor sistemului. La ieșirea NE obținem functie periodica, care poate fi extins într-o serie Fourier. În studiul sistemelor neliniare, doar prima componentă armonică este folosită cel mai des, deoarece în majoritatea cazurilor partea liniară a sistemului este un filtru frecvențe joase. Dar pentru a verifica acest lucru și aplicabilitatea acestei metode de cercetare, este necesar să se determine frecvența auto-oscilațiilor în sistem, prin care să se determine în viitor capacitatea părții liniare de a filtra armonicile superioare. Pentru a face acest lucru, construiți răspunsul în frecvență al părții liniare (LP).

Fie LP-ul sistemului un filtru trece-jos și vom presupune că oscilațiile la intrarea elementului neliniar al NE sunt sinusoidale, atunci semnalul de ieșire al NE este:

Unde A lași VC sunt coeficienții expansiunii Fourier ai funcției neliniare:

Dacă caracteristica neliniară este simetrică și neutră, atunci coeficientul de expansiune al seriei Fourier VC=0 și nu există armonici pare în expansiune:

Folosind aceste relații, exprimăm valoarea sinusului și cosinusului în termeni de semnal de intrare

Să substituim aceste relații în ecuația pentru ieșirea NE și să luăm în considerare doar prima armonică.

Scriem această ecuație sub formă de operator:

Coeficientul A 0 - amplitudinea autooscilațiilor; q este coeficientul de liniarizare armonică în raport cu componenta sinusoidală, depinde de amplitudinea semnalului la intrarea NE; b 1 este coeficientul de liniarizare armonică în raport cu componenta cosinus; ω 0 este amplitudinea auto-oscilațiilor.

În absența unei componente constante la intrarea NE, obținem o ecuație pentru descrierea comportamentului NE:

Aceasta este ecuația de liniarizare armonică NE.

Un NE liniarizat armonic poate fi reprezentat ca:

În acest caz, putem deriva funcția de transfer pentru NE:

în absenţa unei componente constante la intrare.

Coeficientul A 0 - amplitudinea autooscilațiilor;

q este coeficientul de liniarizare armonică în raport cu componenta sinusoidală, depinde de amplitudinea semnalului la intrarea NE;

b 1 este coeficientul de liniarizare armonică în raport cu componenta cosinus;

ω 0 este amplitudinea auto-oscilațiilor.

Partea liniară a sistemului este afectată de semnalul de ieșire NE, care conține întregul spectru de frecvență al expansiunii Fourier. În virtutea principiului suprapunerii, putem presupune că fiecare armonică acționează asupra părții liniare independent de cealaltă. Prin urmare, la ieșirea sistemului pot fi setate oscilații periodice, care vor conține întregul spectru de frecvențe corespunzătoare semnalului NE, dar amplitudinea fiecărei armonici va fi determinată de coeficientul de conversie al părții drepte pentru armonica considerată ( ).

Prin înlocuirea răspunsului în frecvență al părții liniare, puteți seta raportul modificărilor de amplitudine pentru fiecare armonică și puteți verifica dacă partea liniară a LPF este (dacă armonicile mai mari pot fi eliminate).

Dacă se setează frecvența autooscilațiilor și se cunosc coeficienții de liniarizare a armonicii NE, luând în considerare doar prima armonică, atunci frecvența (frecvența primei armonice). Dacă atunci puteți renunța la armonicile superioare și această metodă este potrivită. Acestea. este posibil să se limiteze la calculul unei singure armonice la ieșirea NE. Apoi, pentru o caracteristică impară cu o singură valoare, NE va avea:

Pentru caracteristica impară de histerezis:

În primul caz, NE este echivalent cu o legătură inerțială cu unele particularități - coeficientul de proporționalitate depinde de amplitudinea sau frecvența semnalului la intrarea NE.

În cazul neliniarității histeretice, legătura este echivalentă cu legătura de amplificare. Particularitatea acestei metode de liniarizare face posibilă utilizarea metodelor de frecvență ale teoriei liniare pentru analiza unui sistem neliniar.

Ideea metodei de liniarizare armonică îi aparține lui N.M. Krylov și N.N. Bogolyubov și se bazează pe înlocuirea unui element neliniar al sistemului cu o legătură liniară, ai cărui parametri sunt determinați sub o acțiune de intrare armonică din condiția egalității amplitudinilor primelor armonice la ieșirea elementului neliniar și echivalentul acestuia. legătură liniară. Această metodă poate fi utilizată atunci când partea liniară a sistemului este un filtru trece-jos, de ex. filtrează toate componentele armonice care apar la ieșirea elementului neliniar, cu excepția primei armonice.

Coeficienți de liniarizare armonică și câștiguri complexe echivalente ale elementelor neliniare. Într-un sistem neliniar (Fig. 2.1), parametrii părții liniare și ai elementului neliniar sunt aleși în așa fel încât să existe oscilații periodice simetrice cu o frecvență w.

În centrul metodei de liniarizare armonică a neliniarităților (Fig. 2.10), descrisă de ecuația

y n = F(x), (2,17)

se presupune că la intrarea unui element neliniar se aplică o acțiune armonică cu o frecvență w și o amplitudine A, adică

x= A sin y, unde y = wt, (2.18)

și numai prima armonică se distinge de întregul spectru al semnalului de ieșire

y n 1 = A n 1 sin(y + y n 1), (2.19)

Unde A n 1 - amplitudine și y n 1 - defazare;

în acest caz, armonicile superioare sunt eliminate și se stabilește o conexiune între prima armonică a semnalului de ieșire și efectul armonic de intrare al elementului neliniar.

Orez. 2.10. Caracteristicile unui element neliniar

În cazul insensibilității sistemului neliniar la armonici superioare, elementul neliniar poate fi, în prima aproximare, înlocuit cu un element cu un câștig echivalent, care determină prima armonică de oscilații periodice la ieșire în funcție de frecvență. și amplitudinea oscilațiilor sinusoidale la intrare.

Pentru elementele neliniare cu caracteristica (2.17), ca urmare a extinderii funcției periodice F(x) într-o serie Fourier cu oscilații sinusoidale la intrare (2.18), obținem o expresie pentru prima armonică a semnalului de ieșire

y n 1 = b 1F siny + a 1F confortabil, (2.20)

unde b 1F , a 1F - coeficienții de expansiune într-o serie Fourier, care determină amplitudinile componentelor în fază și, respectiv, în cuadratura ale primei armonice, care sunt determinate de formulele:

px= A w cos y, unde p = d/dt,

atunci relația dintre prima armonică a oscilațiilor periodice la ieșirea elementului neliniar și oscilațiile sinusoidale la intrarea sa poate fi scrisă ca

y н 1 = x, (2,21)

unde q = b 1F / A, q¢ = a 1F / A.

Ultima ecuație se numește ecuația de liniarizare armonică, iar coeficienții q și q¢ - coeficienţii de liniarizare armonică.

Astfel, un element neliniar, atunci când este expus unui semnal armonic, este descris prin ecuația (2.21), care este liniară, până la armonici superioare. Această ecuație a unui element neliniar diferă de ecuația unei legături liniare prin faptul că coeficienții ei q și q¢ se modifică odată cu modificarea amplitudinii Aşi frecvenţa w a oscilaţiilor la intrare. Aceasta este diferența fundamentală dintre liniarizarea armonică și liniarizarea convențională, ai căror coeficienți nu depind de semnalul de intrare, ci sunt determinați numai de tipul de caracteristică a elementului neliniar.

Pentru diferite tipuri de caracteristici neliniare, coeficienții de liniarizare armonică sunt rezumați în tabel. În cazul general, coeficienții de liniarizare armonică q( A, w) și q¢( A, w) depind de amplitudine Aşi frecvenţa w a oscilaţiilor la intrarea elementului neliniar. Cu toate acestea, pentru neliniaritățile statice acești coeficienți q( A) și q¢( A) sunt doar o funcție a amplitudinii A semnal armonic de intrare, iar pentru neliniaritățile statice cu o singură valoare, coeficientul q¢( A) = 0.

Supunând ecuația (2.21) transformării Laplace în condiții inițiale zero și apoi înlocuind operatorul s cu jw (s = jw), obținem câștig complex echivalent element neliniar

W E (jw, A) = q + jq¢ = A e (w, A) e j y e (w , A) , (2.22)

unde modulul și argumentul câștigului complex echivalent sunt legate de coeficienții de liniarizare armonică prin expresii

A E (w, A) = mod W E (jw, A) =

y E (w, A) = arg W E (jw, A) = arctg.

Coeficientul de transfer complex echivalent al unui element neliniar face posibilă determinarea amplitudinii și defazajului primei armonici (2.19) la ieșirea elementului neliniar sub acțiunea armonică (2.18) la intrarea sa, i.e.

A n 1 = A„A E (w, A); y n 1 \u003d y E (w, A).

Studiul regimurilor periodice simetrice în sisteme neliniare.În studiul sistemelor neliniare bazate pe metoda liniarizării armonice, în primul rând, se rezolvă problema existenței și stabilității modurilor periodice. Dacă regimul periodic este stabil, atunci există auto-oscilații în sistem cu frecvența w 0 și amplitudine A 0 .

Considerăm un sistem neliniar (Fig. 2.5), care include o parte liniară cu o funcție de transfer

și un element neliniar cu un câștig complex echivalent

W E (jw, A) = q(w, A) + jq¢(w, A) = A E (w, A) e j y e (w , A) . (2.24)

Luând în considerare expresia (2.21), putem scrie ecuația sistemului neliniar

(A(p) + B(p)´)x = 0. (2.25)

Dacă apar autooscilații într-un sistem neliniar închis

x= A 0 sin w 0 t

cu o amplitudine și o frecvență constante, atunci coeficienții de liniarizare armonică se dovedesc a fi constanți, iar întregul sistem este staționar. Pentru a evalua posibilitatea auto-oscilațiilor într-un sistem neliniar folosind metoda liniarizării armonice, este necesar să se găsească condițiile pentru limita de stabilitate, așa cum sa făcut în analiza stabilității sistemelor liniare. O soluție periodică există dacă A = A 0 și w = w 0 ecuație caracteristică a unui sistem liniarizat armonic

A(p) + B(p)´ = 0 (2,26)

are o pereche de rădăcini imaginare l i = jw 0 și l i +1 = -jw 0 . Stabilitatea soluției trebuie evaluată suplimentar.

În funcție de metodele de rezolvare a ecuației caracteristice, se disting metode de studiere a sistemelor neliniare.

Metoda analitica. Pentru a estima posibilitatea auto-oscilațiilor într-un sistem neliniar, jw este înlocuit în polinomul caracteristic liniarizat armonic al sistemului în loc de p

D(jw, A) = A(jw) + B(jw)´. (2,27)

Rezultatul este ecuația D(jw, A) = 0, ai cărui coeficienți depind de amplitudinea și frecvența regimului auto-oscilator presupus. Separarea părților reale și imaginare

Re D(jw, A) = X(w, A);

sunt D(jw, A) = Y(w, A),

obținem ecuația

X(w, A) + jY(w, A) = 0. (2.28)

Dacă pentru valori reale A 0 și w 0 expresia (2.28) este satisfăcută, atunci este posibil un mod auto-oscilator în sistem, ai cărui parametri sunt calculați conform următorului sistem de ecuații:

Din expresiile (2.29), se poate găsi dependența amplitudinii și frecvenței auto-oscilațiilor de parametrii sistemului, de exemplu, de coeficientul de transfer k al părții liniare a sistemului. Pentru a face acest lucru, este necesar în ecuațiile (2.29) să se considere coeficientul de transfer k ca o variabilă, i.e. scrieți aceste ecuații sub forma:

Conform graficelor A 0 = f(k), w 0 = f(k), puteți alege coeficientul de transfer k, la care amplitudinea și frecvența posibilelor auto-oscilații au valori acceptabile sau sunt complet absente.

metoda frecvenței. În conformitate cu criteriul de stabilitate Nyquist, oscilațiile neamortizate într-un sistem liniar apar atunci când caracteristica amplitudine-fază a unui sistem în buclă deschisă trece printr-un punct cu coordonatele [-1, j0]. Această condiție este și o condiție pentru existența auto-oscilațiilor într-un sistem neliniar liniarizat armonic, i.e.

W n (jw, A) = -1. (2.31)

Deoarece părțile liniare și neliniare ale sistemului sunt conectate în serie, răspunsul în frecvență al unui sistem neliniar în buclă deschisă are forma

W n (jw, A) = W lch (jw)´W E (jw, A). (2.32)

Atunci, în cazul unei caracteristici statice a unui element neliniar, condiția (2.31) ia forma

W lch (jw) = - . (2,33)

Soluția ecuației (2.33) cu privire la frecvența și amplitudinea auto-oscilațiilor poate fi obținută grafic ca punct de intersecție al hodografului răspunsului în frecvență al părții liniare a sistemului W lch (jw) și hodograful caracteristică inversă a părții neliniare, luată cu semnul opus (Fig. 2.11). Dacă aceste hodografe nu se intersectează, atunci regimul auto-oscilațiilor nu există în sistemul studiat.

Orez. 2.11. Hodografe ale părților liniare și neliniare ale sistemului

Pentru stabilitatea regimului auto-oscilator cu frecvenţa w 0 şi amplitudine A 0 se cere ca punctul de pe hodograful părții neliniare - , corespunzător amplitudinii crescute A 0+D A comparativ cu valoarea în punctul de intersecție a hodografelor, nu a fost acoperit de hodograful răspunsului în frecvență al părții liniare a sistemului și punctul corespunzător amplitudinii reduse a fost acoperit A 0-D A.

Pe fig. 2.11 oferă un exemplu de locație a hodografelor pentru cazul în care există auto-oscilații stabile într-un sistem neliniar, deoarece A 3 < A 0 < A 4 .

Studiu asupra răspunsurilor în frecvență logaritmică.

Când se studiază sisteme neliniare prin caracteristici de frecvență logaritmică, condiția (2.31) este rescrisă separat pentru modulul și argumentul câștigului complex echivalent al unui sistem neliniar în buclă deschisă.

mod W lch (jw)W e (jw, A) = 1;

arg W lch (jw)W e (jw, A) = - (2k+1)p, pentru k=0, 1, 2, ...

cu trecerea ulterioară la caracteristicile de amplitudine și fază logaritmice

L h (w) + L e (w, A) = 0; (2.34)

y lch (w) + y e (w, A) = - (2k+1)p, pentru k=0, 1, 2, ... (2.35)

Condițiile (2.34) și (2.35) ne permit să determinăm amplitudinea A 0 și frecvența w 0 a soluției periodice a ecuației (2.25) conform caracteristicilor logaritmice ale părții liniare a sistemului L lch (w), y lch (w) și elementului neliniar L e (w, A), y e (w, A).

Autooscilații cu frecvența w 0 și amplitudine A 0 va exista într-un sistem neliniar dacă soluția periodică a ecuației (2.25) este stabilă. O metodă aproximativă pentru studierea stabilității unei soluții periodice este de a studia comportamentul sistemului la o frecvență w = w 0 și valori de amplitudine A =A 0+D Ași A =A 0-D A, unde D A> 0 - increment mic de amplitudine. Când se studiază stabilitatea unei soluţii periodice pt A 0+D Ași A 0-D A după caracteristicile logaritmice se utilizează criteriul de stabilitate Nyquist.

În sistemele neliniare cu caracteristici statice cu o singură valoare ale unui element neliniar, coeficientul de liniarizare armonică q¢( A) este egal cu zero și, prin urmare, egal cu zero și defazarea y e ( A) contribuit de element. În acest caz, soluția periodică a ecuației sistemului

x = 0 (2,36)

există dacă sunt îndeplinite următoarele condiții:

L h (w) \u003d - L e ( A); (2.37)

y lch (w) = - (2k+1)p, pentru k=0, 1, 2, ... (2,38)

Ecuația (2.38) ne permite să determinăm frecvența w \u003d w 0 a unei soluții periodice, iar ecuația (2.37) - amplitudinea acesteia A =A 0 .

Cu o parte liniară relativ simplă, soluțiile acestor ecuații pot fi obținute analitic. Cu toate acestea, în majoritatea cazurilor este recomandabil să le rezolvăm grafic (Fig. 2.12).

Când se studiază stabilitatea unei soluții periodice a ecuației (2.36), i.e. atunci când se determină existența auto-oscilațiilor într-un sistem neliniar cu o caracteristică statică neliniară cu o singură valoare, se utilizează criteriul Nyquist: soluţie periodică cu frecvenţa w = w 0 şi amplitudine A =A 0 este stabil dacă, pe măsură ce frecvența se schimbă de la zero la infinit și o creștere pozitivă a amplitudinii D A> 0 diferența dintre numărul de tranziții pozitive (de sus în jos) și negative (de jos în sus) ale caracteristicii de fază a părții liniare a sistemului y lch (w) prin linia -p este zero în frecvență interval, unde L lch (w)³-L e (w 0 , A 0+D A), și nu este egal cu zero în domeniul de frecvență, unde L h (w)³-L e (w 0, A 0-D A).

Pe fig. 2.12 prezintă un exemplu de determinare a soluțiilor periodice într-un sistem neliniar cu o constrângere. Într-un astfel de sistem, există trei soluții periodice cu frecvențele w 01 , w 02 și w 03 , determinate în punctele de intersecție a caracteristicii de fază y lch (w) cu dreapta -180 0 . Amplitudini periodice ale soluției A 01 , A 02 și A 03 sunt determinate din condiția (2.37) de caracteristicile de amplitudine logaritmică ale elementului neliniar -L e (w 01 , A), -L e (w 02, A) și -L e (w 03, A).

Orez. 2.12. Amplitudinea logaritmică și caracteristicile de fază

Dintre cele trei soluții definite în Fig. 2.12, două sunt stabile. Soluție cu frecvența w = w 01 și amplitudine A =A 01 este stabil, deoarece în domeniul de frecvență 1, unde L lch (w)³-L e (w 01, A 01+D A), caracteristica de fază y lch (w) nu traversează linia -180 0, ci în intervalul de frecvență 2, unde L lch (w)³-L e (w 01, A 01-D A), caracteristica de fază y lch (w) traversează odată linia -180 0 . Soluție cu frecvența w = w 02 și amplitudine A =A 02 este instabil, deoarece în domeniul de frecvență în care L h (w)³-L e (w 02, A 02+D A), caracteristica de fază y lch (w) traversează odată linia -180 0 . Soluție periodică de înaltă frecvență cu frecvența w = w 03 și amplitudine A =A 03 este stabil, deoarece în domeniul de frecvență, unde L h (w)³-L e (w 03, A 03+D A), există o tranziție pozitivă și una negativă a caracteristicii de fază y lch (w) prin linia -180 0 și în domeniul de frecvență în care L lch (w)³-L e (w 03, A 03-D A), există două tranziții pozitive și una negativă a caracteristicii de fază y lch (w) prin linia -180 0 .

În sistemul considerat, cu mici perturbații, autooscilații de înaltă frecvență cu frecvența w 03 și amplitudine A 03 , iar pentru perturbații mari - auto-oscilații de joasă frecvență cu frecvența w 01 și amplitudine A 01 .

Exemplu. Investigați modurile auto-oscilante într-un sistem neliniar, a cărui parte liniară are următoarea funcție de transfer

unde k=200 s-1; T1 = 1,5 s; T 2 \u003d 0,015 s,

iar ca element neliniar se folosește un releu cu zonă moartă (Fig. 2.4, b) la c=10 V, b=2 V.

Soluție Conform tabelului pentru un releu cu zonă moartă, găsim coeficienții de liniarizare armonică:

La A³ b, q¢( A) = 0.

La construirea caracteristicilor unui element neliniar, este recomandabil să se folosească valoarea relativă a amplitudinii efectului armonic de intrare m = A/b. Să rescriem expresia pentru coeficientul de liniarizare armonică în formă

unde este coeficientul de transmisie al releului;

Amplitudine relativă.

Coeficientul de transfer al releului k n este legat de partea liniară a sistemului și obținem coeficienții de liniarizare armonici normalizați

iar amplitudinea logaritmică normalizată caracteristică elementului releu cu semnul opus

Dacă m® 1, atunci -L e (m)® ¥; iar când m >> 1 -L e (m) = 20 lg m. Astfel, asimptotele caracteristicii amplitudinii logaritmice normalizate cu semnul opus sunt dreapta verticală și dreapta cu o pantă de +20 dB/dek, care trec prin punctul cu coordonatele L = 0, m = 1 (Fig. 2.13).

Orez. 2.13. Determinarea unei soluții periodice într-un sistem de relee

cu zona moarta

A 0 = b´m 1 = = 58 V.

Pentru a rezolva problema existenței auto-oscilațiilor în conformitate cu caracteristica de amplitudine logaritmică normalizată cu semnul opus al elementului neliniar și funcția de transfer a părții liniare a sistemului

în fig. 2.13 a reprezentat grafic caracteristicile logaritmice ale L ch (w), -L e (m) și y ch (w).

Frecvența soluției periodice w 0 = 4,3 s -1 se determină în punctul de intersecție a caracteristicii de fază y lch (w) și a dreptei -180 0 . Amplitudinile solutiilor periodice m 1 = 29 si m 2 = 1,08 se gasesc dupa caracteristicile L h (w) si -L e (m). O soluție periodică cu o amplitudine mică m 2 este instabilă, în timp ce o soluție periodică cu o amplitudine mare m 1 este stabilă.

Astfel, în sistemul de relee studiat, există un mod auto-oscilator cu o frecvență w 0 = 4,3 s -1 și o amplitudine A 0 = b´m 1 = = 58 V.

Ministerul Educației și Științei al Federației Ruse

Universitatea Tehnică de Stat din Saratov

Institutul de Inginerie, Tehnologie și Management Balakovo

Metoda liniarizării armonice

Ghid pentru lucrul de laborator la cursul „Teorie control automat» pentru studenții specialității 210100

Aprobat

consiliul editorial și editorial

Institutul de Tehnologie Balakovo,

tehnologie si management

Balakovo 2004

Scopul lucrării: Studiul sistemelor neliniare folosind metoda liniarizării armonice (echilibrul armonic), determinarea coeficienților de liniarizare armonică pentru diverse legături neliniare. Obținerea deprinderilor în găsirea parametrilor oscilațiilor simetrice de amplitudine și frecvență constante (auto-oscilații), folosind metode algebrice, frecvenței, precum și utilizarea criteriului Mikhailov.

INFORMATII DE BAZA

Metoda liniarizării armonice se referă la metode aproximative de studiere a sistemelor neliniare. Face posibilă evaluarea stabilității sistemelor neliniare destul de simplu și cu o acuratețe acceptabilă și determinarea frecvenței și amplitudinii oscilațiilor stabilite în sistem.

Se presupune că ACS neliniar investigat poate fi reprezentat în următoarea formă

în plus, partea neliniară trebuie să aibă o singură neliniaritate

. (1)

Această neliniaritate poate fi fie continuă, fie releu, fără ambiguitate sau histeretică.

Orice funcție sau semnal poate fi extins într-o serie conform unui sistem de funcții ortonormale liniar independente, într-un caz particular. Seria Fourier poate fi folosită ca atare serie ortogonală.

Să extindem semnalul de ieșire al părții neliniare a sistemului într-o serie Fourier

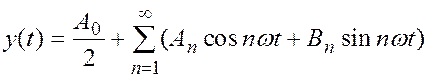, (2)

aici sunt coeficienții Fourier,

,

,

. (3)

Astfel, semnalul conform (2) poate fi reprezentat ca o sumă infinită de armonici cu frecvențe crescătoare. etc. Acest semnal este introdus în partea liniară a sistemului neliniar.

Să notăm funcția de transfer a părții liniare

, (4)

iar gradul polinomului numărătorului trebuie să fie mai mic decât gradul polinomului numitorului. În acest caz, răspunsul în frecvență al părții liniare are forma

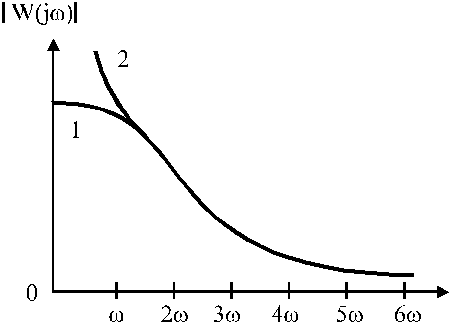
unde 1 - nu are poli, 2 - are un stâlp sau poli.

Pentru răspunsul în frecvență, este corect să scrieți

Astfel, partea liniară a sistemului neliniar este un filtru trece-înalt. În acest caz, partea liniară va trece doar frecvențele joase fără atenuare, în timp ce frecvențele înalte vor fi atenuate semnificativ pe măsură ce frecvența crește.

Metoda de liniarizare armonică presupune că partea liniară a sistemului va trece doar componenta DC a semnalului și prima armonică. Apoi semnalul de la ieșirea părții liniare va arăta ca

Acest semnal trece prin întreaga buclă închisă a sistemului Fig.1 și la ieșirea elementului neliniar fără a ține cont de armonici superioare, conform (2) avem

. (7)

În studiul sistemelor neliniare folosind metoda liniarizării armonice sunt posibile cazuri de oscilații simetrice și asimetrice. Să luăm în considerare cazul oscilațiilor simetrice. Aici și.

Introducem urmatoarea notatie

,

.

Înlocuindu-le în (7), obținem . (opt)

Ținând cont de faptul că

,

, Unde ,

. (9)

Conform (3) și (8) la

,

. (10)

Expresia (9) este o liniarizare armonică a neliniarității stabilește o relație liniară între variabila de intrare și variabila de ieșire la . Mărimile și se numesc coeficienți de liniarizare armonică.

Trebuie remarcat faptul că ecuația (9) este liniară pentru anumite valori și (amplitudini și frecvențe ale oscilațiilor armonice în sistem). Dar, în general, păstrează proprietăți neliniare, deoarece coeficienții sunt diferiți pentru diferite și . Această caracteristică ne permite să explorăm proprietățile sistemelor neliniare folosind metoda liniarizării armonice [Popov E.P.].

În cazul oscilațiilor asimetrice, liniarizarea armonică a neliniarității conduce la ecuația liniară

,

,

. (12)

La fel ca și ecuația (9), ecuația liniarizată (11) păstrează proprietățile unui element neliniar, deoarece coeficienții de liniarizare armonică , , precum și componenta constantă depind atât de deplasarea, cât și de amplitudinea oscilațiilor armonice .

Ecuațiile (9) și (11) permit obținerea funcțiilor de transfer ale elementelor neliniare liniarizate armonic. Deci pentru vibrații simetrice

După cum sa menționat deja, în ACP-uri neliniare și, în special, releu, sunt adesea observate oscilații periodice stabile amplitudine și frecvență constante, așa-numitele autooscilații. Mai mult, auto-oscilațiile pot persista chiar și cu modificări semnificative ale parametrilor sistemului. Practica a arătat că în multe cazuri fluctuațiile valorii reglate (Fig. 3) sunt apropiate de armonice.

Apropierea autooscilațiilor de cele armonice face posibilă utilizarea metodei liniarizării armonice pentru determinarea parametrilor acestora – amplitudinea A și frecvența w 0 . Metoda se bazează pe presupunerea că partea liniară a sistemului este un filtru trece-jos (ipoteza filtrului). Să determinăm condițiile în care auto-oscilațiile din sistem pot fi apropiate de cele armonice. Ne restrângem la sisteme care, ca în Fig. 3 poate fi redusă la o legătură în serie a unui element neliniar și a unei piese liniare. Presupunem că semnalul de referință este o valoare constantă; pentru simplitate, îl vom lua egal cu zero. Și semnalul de eroare (Figura 3) este armonic:

Semnalul de ieșire al unui element neliniar, ca orice semnal periodic - în Figura 3 acestea sunt oscilații dreptunghiulare - poate fi reprezentat ca suma armonicilor din seria Fourier.

Să presupunem că partea liniară a sistemului este un filtru trece-jos (Fig. 4) și trece doar prima armonică cu frecvența w 0 . Al doilea cu o frecvență de 2w 0 și armonici mai mari sunt filtrate de partea liniară. În acest caz, pe ieșire liniară piese vor exista practic doar prima armonică , iar influența armonicilor superioare poate fi neglijată

Astfel, dacă partea liniară a sistemului este un filtru trece-jos, iar frecvența de auto-oscilație w 0 satisface condițiile

, (4)

Se numește ipoteza că partea liniară a sistemului este un filtru trece-jos ipoteza filtrului . Ipoteza filtrului este întotdeauna satisfăcută dacă diferența dintre gradele polinoamelor numitorului și numărătorului funcției de transfer a părții liniare

cel putin doua

Condiția (6) este îndeplinită pentru multe sisteme reale. Un exemplu este legătura aperiodică de ordinul doi și integrarea reală

Când se studiază auto-oscilațiile care sunt apropiate de armonică, se ia în considerare doar prima armonică a oscilațiilor periodice la ieșirea unui element neliniar, deoarece armonicile superioare sunt oricum filtrate de partea liniară. În modul de auto-oscilare, liniarizare armonică element neliniar. Elementul neliniar este înlocuit cu un element liniar echivalent cu câștig complex (funcția de descriere) în funcție de amplitudinea semnalului armonic de intrare:

unde și sunt părțile reale și imaginare ale ,

- argument,

- modul.

În cazul general, depinde atât de amplitudinea, cât și de frecvența auto-oscilațiilor și de componenta constantă. Câștig de element neliniar complex din punct de vedere fizic, denumit mai frecvent coeficient de liniarizare armonică , există câștig complex al elementului neliniar în prima armonică. Modulul coeficientului de liniarizare armonică

numeric egal cu raportul dintre amplitudinea primei armonice la ieșirea elementului neliniar și amplitudinea semnalului armonic de intrare.

Argument

caracterizează defazajul dintre prima armonică a oscilațiilor de ieșire și semnalul armonicii de intrare. Pentru neliniaritățile cu o singură valoare, cum ar fi, de exemplu, în Fig. 2a și 2b, expresia reală și

Pentru neliniarități ambigue, fig. 2, c, 2, d, este determinată de formula

unde S este aria buclei de histerezis. Zona S este luată cu semnul plus dacă bucla de histerezis este ocolită în sens pozitiv (Fig. 2c) și cu semnul minus în caz contrar (Fig. 2d).

În cazul general, și sunt calculate prin formule

unde , este o funcție neliniară (caracteristică unui element neliniar).

Având în vedere cele de mai sus, în studiul autooscilațiilor apropiate de armonică, ASR neliniar (Fig. 3) este înlocuit cu unul echivalent cu un coeficient de liniarizare armonică în locul unui element neliniar (Fig. 5). Semnalul de ieșire al elementului neliniar din fig. 5 este marcat ca, este

Subliniază că elementul neliniar generează numai

prima armonică a vibraţiilor. Formulele pentru coeficienții de liniarizare armonică pentru neliniaritățile tipice pot fi găsite în literatură, de exemplu, în. Tabelul din Anexa B prezintă caracteristicile elementelor releului studiate, formulele și hodografele acestora. Există, de asemenea, formule și hodografe pentru coeficientul reciproc de liniarizare armonică, definit prin expresia

unde sunt părțile reale și imaginare ale . Hodografele și sunt reprezentate în coordonatele și, respectiv.

Să scriem acum condițiile de existență a auto-oscilațiilor. Sistemul din fig. 5 este echivalent cu liniar. Într-un sistem liniar, există oscilații neamortizate dacă se află la limita stabilității. Să folosim condiția limitei de stabilitate după criteriul Nyquist: . Pe fig. 6a – două puncte de intersecție, ceea ce indică prezența a două cicluri limită.

Metoda liniarizării armonice permite studierea stabilității și acurateței sistemelor neliniare cu suficientă precizie pentru practică, folosind metode dezvoltate pentru sisteme liniare. Metoda face posibilă determinarea prezenței auto-oscilațiilor, precum și frecvența și amplitudinea acestora.

Un sistem neliniar este reprezentat ca o combinație între o parte liniară și una neliniară (Fig. 5).

Orez. 5 Diagrama unui sistem neliniar

Semnalul de ieșire al părții neliniare a sistemului este determinat în general de expresie

Notați ca funcție de transfer a părții liniare. Sistemul de ecuații ia forma

Să găsim condițiile în care apar oscilații armonice de formă la ieșirea părții liniare a sistemului

În acest caz, semnalul YT) partea neliniară va fi, de asemenea, o funcție periodică, dar diferită de o sinusoidă. Această funcție poate fi extinsă într-o serie Fourier

În această expresie A iși b i- coeficienții Fourier. Pentru neliniarități simetrice F 0 =0.

Condiția principală pe care metoda o impune părții liniare a sistemului este starea filtrului trece-jos. Se crede că partea liniară trece doar prima armonică de oscilații. Această ipoteză ne permite să considerăm armonicile superioare din (7.19) nesemnificative și să ne limităm la a considera doar prima armonică a semnalului YT).

atunci expresia (7.20) poate fi rescrisă ca

Prima ecuație a sistemului (7.17) ia forma

În această expresie

Rezultatul înlocuirii neliniarității F(x, sx) expresie

și se numește liniarizare armonică. Cantitati qși q 1 se numesc coeficienți de liniarizare armonică sau pur și simplu coeficienți armonici. Pentru neliniarități cu o singură valoare, de obicei q 1 =0 . Formulele pentru coeficienții armonici corespunzători neliniarităților tipice sunt date în anexe.

Diferența fundamentală dintre liniarizarea armonică și liniarizarea convențională este aceea că, la liniarizarea convențională, caracteristica neliniară este înlocuită cu o linie dreaptă cu o anumită pantă constantă, iar la liniarizarea armonică, cu o linie dreaptă, a cărei pantă depinde de amplitudinea semnalul de intrare al elementului neliniar.

Luați în considerare metoda de determinare a amplitudinii și frecvenței auto-oscilațiilor.

unu). În ecuația caracteristică a sistemului obținut din (7.22) facem modificarea s=j si ia

2). Din expresia rezultată, selectăm părțile reale și imaginare și le echivalăm cu zero, ceea ce, conform criteriului Mihailov, corespunde că sistemul se află pe limita stabilității oscilatorii.

• 3). Soluția acestui sistem oferă frecvența și valorile coeficienților armonici. Dacă aceste valori sunt reale și pozitive, atunci sistemul are un ciclu limită. Valorile coeficienților armonici pot fi utilizate pentru a determina amplitudinea ciclului limită.
• 4). Un semn general al stabilității ciclului limită, de ex. existența auto-oscilațiilor, este egalitatea la zero a penultimului determinant Hurwitz pentru valorile obținute ale amplitudinii și frecvenței ciclului limită. Este adesea mai convenabil să folosiți condiția de stabilitate a ciclului limită pe baza criteriului de stabilitate al lui Mihailov.

Dacă această inegalitate este satisfăcută, atunci ciclul limită este stabil și există auto-oscilații în sistem cu amplitudinea și frecvența definite mai sus. Indicele ”*” înseamnă că derivatele sunt calculate cu valori deja cunoscute ale coeficienților armonici, amplitudinii și frecvenței.

Exemplu. Să presupunem că în sistemul de stabilizare a unghiului de inclinare a avionului deja considerat mai sus, mecanismul de guvernare este neliniar și diagrama bloc are forma prezentată în Fig. 7.6.

Fig.6 Diagrama unui sistem de direcție neliniar

Să setăm următorii parametri ai neliniarității caracteristicilor de viteză ale sistemului de direcție: b = 0,12, k 1 =tg =c/b = 6,7. Coeficienții de liniarizare armonică ai acestei neliniarități sunt determinați de expresii

Inlocuind caracteristica neliniara din circuit cu un coeficient armonic se obtine functia de transfer a mecanismului de directie

Inlocuim aceasta functie de transfer in diagrama bloc a sistemului de stabilizare a unghiului de pas si determinam functia de transfer a sistemului inchis.

În ecuația caracteristică a unui sistem închis, facem schimbarea s = jși selectați părțile reale și imaginare.

Din a doua ecuație a sistemului obținem o expresie pentru frecvența: , iar substituind-o în prima ecuație, după transformări, obținem

Înlocuind aici expresii definite anterior pentru coeficienții ecuației caracteristice, se poate obține o ecuație pătratică față de coeficientul armonic, rezolvând care, găsim

Din aceste valori este posibil să se calculeze pentru două cazuri toți coeficienții ecuației caracteristice și să se determine frecvențele corespunzătoare fiecărei valori q(A). Primim:

Ambele valori ale coeficientului armonic și frecvențele corespunzătoare sunt reale și pozitive. Prin urmare, există două cicluri limită în sistem. Valorile amplitudinii ciclului limită sunt determinate numeric prin selectarea unei astfel de valori la care formula pentru coeficientul de liniarizare armonică dă o valoare egală cu cea calculată anterior. În cazul luat în considerare, obținem

Acum să estimăm stabilitatea ciclurilor limită. Folosim inegalitatea obținută din criteriul Mihailov, pentru care definim

Derivata coeficientului de liniarizare armonică inclusă în expresiile obţinute se calculează prin formula

Calculele folosind formulele de mai sus arată că primul ciclu limită nu este stabil și apare când (0) 0.1166(6.7 0 ). Dacă abaterea inițială este mai mică decât cea specificată, atunci procesul de la intrarea elementului neliniar decade (Fig. 7. 7) și sistemul este stabil.

Dacă valoarea inițială a unghiului de pas este mai mare decât valoarea specificată, atunci procesele converg către al doilea ciclu limită, care este stabil și, astfel, apar auto-oscilații în sistem (Fig. 8).

Orez. opt

Prin modelare se determină că aria de atracție a unui ciclu limită stabil se află aproximativ în interiorul (0) 0.1167 - 1.4 (6.71 0 - 80.2 0 ).