Гармоническая линеаризация нелинейных элементов. Этот метод используется для исследования нелинейных систем с линейной частью выше третьего порядка. В большинстве систем переходной процесс представляет собой затухающие колебания, поэтому на входе нелинейного элемента по главной обратной связи (ГОС) передаётся периодический сигнал с медленно меняющейся амплитудой и при наличии входного сигнала вместе с постоянной составляющей.

Будем считать, что на входе нелинейного элемента за некоторый малый начальный промежуток времени амплитуда и частота не измены или они соответствуют амплитуде и частоте автоколебаний системы. На выходе НЭ получим периодическую функцию, которую можно разложить в ряд Фурье. При исследовании нелинейных систем чаще всего используют только первую гармоническую составляющую, т.к. в большинстве случаев линейная часть системы является фильтром низких частот. Но для того что бы проверить это и возможности применимости этого метода исследований необходимо определить частоту автоколебаний в системе, по которой в дальнейшем определить способность линейной части отфильтровывать высшие гармоники. Для этого строят АЧХ линейной части (ЛЧ).

Пусть ЛЧ системы является фильтром НЧ, и будем считать, что колебания на входе нелинейного элемента НЭ синусоидальные, тогда выходным сигналом НЭ:

где А к и В к – коэффициенты разложения Фурье нелинейной функции:

Если нелинейная характеристика симметрична и нейтральна, то коэффициент разложения ряда Фурье В к =0 и в разложении отсутствуют чётные гармоники:

Используя эти соотношения, выразим значение синуса и косинуса через входной сигнал

Подставим эти соотношения в уравнение для выхода НЭ и учтём только первую гармонику.

Запишем это уравнение в операторной форме:

Коэффициент А 0 – амплитуда автоколебаний; q – коэффициент гармонической линеаризации по синусоидальной составляющей, он зависит от амплитуды сигнала на входе НЭ; b 1 – коэффициент гармонической линеаризации по косинусоидальной составляющей; ω 0 – амплитуда автоколебаний.

При отсутствии постоянной составляющей на входе НЭ мы получим уравнение описания поведения НЭ:

Это уравнение гармонической линеаризации НЭ.

Гармонически линеаризованный НЭ можно представить в виде:

В этом случае мы можем вывести передаточную функцию для НЭ:

при отсутствии постоянной составляющей на входе.

Коэффициент А 0 – амплитуда автоколебаний;

q – коэффициент гармонической линеаризации по синусоидальной составляющей, он зависит от амплитуды сигнала на входе НЭ;

b 1 – коэффициент гармонической линеаризации по косинусоидальной составляющей;

ω 0 – амплитуда автоколебаний.

На линейную часть системы действует выходной сигнал с НЭ, который содержит весь спектр частот разложения Фурье. В силу принципа суперпозиции можно считать, что каждая гармоника действует на линейную часть независимо от другой. Поэтому на выходе системы могут устанавливаться периодические колебания, которые будут содержать весь спектр частот, соответствующих сигналу НЭ, но амплитуда каждой гармоники будет определяться коэффициентом преобразования правой части по рассмотренной гармонике ().

Подставив АЧХ линейной части можно установить соотношение изменения амплитуд для каждой гармоники и проверить, является ли линейная часть ФНЧ (можно ли отбросить высшие гармоники).

Если установлена частота автоколебаний и известны коэффициенты гармонической линеаризации НЭ, учитывающие только первую гармонику, то частота (частоте первой гармоники). Если то можно отбросить высшие гармоники и этот метод подходит. Т.е. можно ограничиться расчетом только одной гармоники на выходе НЭ. Тогда для однозначной нечётной характеристики НЭ будет иметь:

Для гистерезисной нечётной характеристики:

В первом случае НЭ эквивалентен безинерционному звену с некоторыми особенностями – коэффициент пропорциональности зависит от амплитуды или частоты сигнала на входе НЭ.

В случае с гистерезисной нелинейности звено эквивалентно форсирующему звену. Особенность этого способа линеаризации позволяет использовать для анализа нелинейной системы частотные методы линейной теории.

Идея метода гармонической линеаризации принадлежит Н.М. Крылову и Н.Н. Боголюбову и базируется на замене нелинейного элемента системы линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Данный метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники.

Коэффициенты гармонической линеаризации и эквивалентные комплексные коэффициенты передачи нелинейных элементов . В нелинейной системе (рис. 2.1) параметры линейной части и нелинейного элемента выбирают таким образом, чтобы существовали симметричные периодические колебания с частотой w.

В основе метода гармонической линеаризации нелинейностей (рис. 2.10), описываемых уравнением

y н = F(x), (2.17)

лежит предположение, что на вход нелинейного элемента подается гармоническое воздействие с частотой w и амплитудой a , т.е.

x = a sin y, где y = wt, (2.18)

а из всего спектра выходного сигнала выделяется только первая гармоника

y н 1 = a н 1 sin(y + y н 1), (2.19)

где a н 1 - амплитуда а y н 1 - фазовый сдвиг;

при этом высшие гармоники отбрасываются и устанавливается связь между первой гармоникой выходного сигнала и входным гармоническим воздействием нелинейного элемента.

Рис. 2.10. Характеристики нелинейного элемента

В случае нечувствительности нелинейной системы к высшим гармоникам нелинейный элемент может быть в первом приближении заменен некоторым элементом с эквивалентным коэффициентом передачи, который определяет первую гармонику периодических колебаний на выходе в зависимости от частоты и амплитуды синусоидальных колебаний на входе.

Для нелинейных элементов с характеристикой (2.17) в результате разложения периодической функции F(x) в ряд Фурье при синусоидальных колебаниях на входе (2.18) получим выражение для первой гармоники сигнала на выходе

y н 1 = b 1F siny + a 1F cosy, (2.20)

где b 1F , a 1F - коэффициенты разложения в ряд Фурье, определяющие амплитуды соответственно синфазной и квадратурной составляющих первой гармоники, которые определяются по формулам:

px = a w cos y, где p = d/dt,

то связь между первой гармоникой периодических колебаний на выходе нелинейного элемента и синусоидальными колебаниями на его входе можно записать в виде

y н 1 = x, (2.21)

где q = b 1F /a , q¢ = a 1F /a .

Последнее уравнение называется уравнением гармонической линеаризации , а коэффициенты q и q¢ - коэффициентами гармонической линеаризации .

Таким образом, нелинейный элемент при воздействии гармонического сигнала с точностью до высших гармоник описывается уравнением (2.21), которое является линейным. Это уравнение нелинейного элемента отличается от уравнения линейного звена тем, что его коэффициенты q и q¢ изменяются при изменении амплитуды a и частоты w колебаний на входе. Именно в этом заключается принципиальное отличие гармонической линеаризации от обычной, коэффициенты которой не зависят от входного сигнала, а определяются только видом характеристики нелинейного элемента.

Для различных видов нелинейных характеристик коэффициенты гармонической линеаризации сведены в таблицу . В общем случае коэффициенты гармонической линеаризации q(a , w) и q¢(a , w) зависят от амплитуды a и частоты w колебаний на входе нелинейного элемента. Однако, для статических нелинейностей эти коэффициенты q(a ) и q¢(a ) являются функцией только амплитуды a входного гармонического сигнала, а для статических однозначных нелинейностей коэффициент q¢(a ) = 0.

Подвергнув уравнение (2.21) преобразованию по Лапласу при нулевых начальных условиях с последующей заменой оператора s на jw (s = jw), получим эквивалентный комплексный коэффициент передачи нелинейного элемента

W Э (jw, a ) = q + jq¢ = A Э (w, a ) e j y э (w , a ) , (2.22)

где модуль и аргумент эквивалентного комплексного коэффициента передачи связаны с коэффициентами гармонической линеаризации выражениями

A Э (w, a ) = mod W Э (jw, a ) =

y Э (w, a ) = arg W Э (jw, A) = arctg.

Эквивалентный комплексный коэффициент передачи нелинейного элемента позволяет определить амплитуду и фазовый сдвиг первой гармоники (2.19) на выходе нелинейного элемента при гармоническом воздействии (2.18) на его входе, т.е.

a н 1 = a ´A Э (w, a ); y н 1 = y Э (w, a ).

Исследование симметричных периодических режимов в нелинейных системах. При исследовании нелинейных систем на основе метода гармонической линеаризации в первую очередь решают вопрос о существовании и устойчивости периодических режимов. Если периодический режим устойчив, то в системе существуют автоколебания с частотой w 0 и амплитудой a 0 .

Рассмотрим нелинейную систему (рис. 2.5), включающую в себя линейную часть с передаточной функцией

и нелинейный элемент с эквивалентным комплексным коэффициентом передачи

W Э (jw, a ) = q(w, a ) + jq¢(w, a ) = A Э (w, a ) e j y э (w , a ) . (2.24)

Принимая во внимание выражение (2.21), можно записать уравнение нелинейной системы

{A(p) + B(p)´}x = 0. (2.25)

Если в замкнутой нелинейной системе возникают автоколебания

x = a 0 sin w 0 t

с постоянной амплитудой и частотой, то коэффициенты гармонической линеаризации оказываются постоянными, а вся система стационарной. Для оценки возможности возникновения автоколебаний в нелинейной системе методом гармонической линеаризации необходимо найти условия границы устойчивости, как это делалась при анализе устойчивости линейных систем. Периодическое решение существует, если при a = a 0 и w = w 0 характеристическое уравнение гармонически линеаризованной системы

A(p) + B(p)´ = 0 (2.26)

имеет пару мнимых корней l i = jw 0 и l i +1 = -jw 0 . Устойчивость решения необходимо оценить дополнительно.

В зависимости от методов решения характеристического уравнения различают методы исследования нелинейных систем.

Аналитический метод . Для оценки возможности возникновения в нелинейной системе автоколебаний в гармонически линеаризованный характеристический полином системы вместо p подставляют jw

D(jw, a ) = A(jw) + B(jw)´. (2.27)

В результате получают уравнение D(jw, a ) = 0, коэффициенты которого зависят от амплитуды и частоты предполагаемого автоколебательного режима. Выделив вещественную и мнимую части

Re D(jw, a ) = X(w, a );

Im D(jw, a ) = Y(w, a ),

получим уравнение

X(w, a ) + jY(w, a ) = 0. (2.28)

Если при действительных значениях a 0 и w 0 выражение (2.28) удовлетворяется, то в системе возможен автоколебательный режим, параметры которого рассчитываются по следующей системе уравнений:

Из выражений (2.29) можно найти зависимость амплитуды и частоты автоколебаний от параметров системы, например, от коэффициента передачи k линейной части системы. Для этого необходимо в уравнениях (2.29) коэффициент передачи k считать переменной величиной, т.е. эти уравнения записать в виде:

По графикам a 0 = f(k), w 0 = f(k) можно выбрать коэффициент передачи k, при котором амплитуда и частота возможных автоколебаний имеет допустимые значения или вообще отсутствует.

Частотный метод . В соответствии с критерием устойчивости Найквиста незатухающие колебания в линейной системе возникают в том случае, когда амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами [-1, j0]. Данное условие является также условием существования автоколебаний в гармонически линеаризованный нелинейной системе, т.е.

W н (jw, a ) = -1. (2.31)

Так как линейная и нелинейная части системы соединены последовательно, то частотная характеристика разомкнутой нелинейной системы имеет вид

W н (jw, a ) = W лч (jw)´W Э (jw, a ). (2.32)

Тогда в случае статической характеристики нелинейного элемента условие (2.31) принимает вид

W лч (jw) = - . (2.33)

Решение уравнения (2.33) относительно частоты и амплитуды автоколебаний можно получить графически как точку пересечения годографа частотной характеристики линейной части системы W лч (jw) и годографа обратной характеристики нелинейной части , взятой с обратным знаком (рис. 2.11). Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует.

Рис. 2.11. Годографы линейной и нелинейной частей системы

Для устойчивости автоколебательного режима с частотой w 0 и амплитудой a 0 требуется, чтобы точка на годографе нелинейной части - , соответствующая увеличенной амплитуде a 0 +Da по сравнению со значением в точке пересечения годографов, не охватывалась годографом частотной характеристики линейной части системы и охватывалась точка, соответствующая уменьшенной амплитуде a 0 -Da .

На рис. 2.11 дан пример расположения годографов для случая, когда в нелинейной системе существуют устойчивые автоколебания, так как a 3 < a 0 < a 4 .

Исследование по логарифмическим частотным характеристикам .

При исследовании нелинейных систем по логарифмическим частотным характеристикам условие (2.31) переписывают отдельно для модуля и аргумента эквивалентного комплексного коэффициента передачи разомкнутой нелинейной системы

mod W лч (jw)W э (jw, a ) = 1;

arg W лч (jw)W э (jw, a ) = - (2k+1)p, при k=0, 1, 2, ...

с последующим переходом к логарифмическим амплитудной и фазовой характеристикам

L лч (w) + L э (w, a ) = 0; (2.34)

y лч (w) + y э (w, a ) = - (2k+1)p, при k=0, 1, 2, ... (2.35)

Условия (2.34) и (2.35) позволяют определить амплитуду a 0 и частоту w 0 периодического решения уравнения (2.25) по логарифмическим характеристикам линейной части системы L лч (w), y лч (w) и нелинейного элемента L э (w, a ), y э (w, a ).

Автоколебания с частотой w 0 и амплитудой a 0 будут существовать в нелинейной системе, если периодическое решение уравнения (2.25) устойчиво. Приближенный метод исследования устойчивости периодического решения заключается в том, что исследуется поведение системы при частоте w = w 0 и значениях амплитуды a = a 0 + Da и a = a 0 - Da , где Da > 0 - малое приращение амплитуды. При исследовании устойчивости периодического решения при a 0 + Da и a 0 - Da по логарифмическим характеристикам пользуются критерием устойчивости Найквиста.

В нелинейных системах с однозначными статическими характеристиками нелинейного элемента коэффициент гармонической линеаризации q¢(a ) равен нулю, а следовательно, равен нулю и фазовый сдвиг y э (a ), вносимый элементом. В этом случае периодическое решение уравнения системы

x = 0 (2.36)

существует, если выполняются условия:

L лч (w) = - L э (a ); (2.37)

y лч (w) = - (2k+1)p, при k=0, 1, 2, ... (2.38)

Уравнение (2.38) позволяет определить частоту w = w 0 периодического решения, а уравнение (2.37) - его амплитуду a = a 0 .

При сравнительно простой линейной части решения этих уравнений могут быть получены аналитически. Однако в большинстве случаев их целесообразно решать графически (рис. 2.12).

При исследовании устойчивости периодического решения уравнения (2.36), т.е. при определении существования автоколебаний в нелинейной системе с однозначной нелинейной статической характеристикой пользуются критерием Найквиста : периодическое решение с частотой w = w 0 и амплитудой a = a 0 устойчиво, если при изменении частоты от нуля до бесконечности и положительном приращении амплитуды Da > 0 разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов фазовой характеристики линейной части системы y лч (w) через линию -p равна нулю в диапазоне частот, где L лч (w)³-L э (w 0 ,a 0 +Da ), и не равна нулю в диапазоне частот, где L лч (w)³-L э (w 0 ,a 0 -Da ).

На рис. 2.12 показан пример определения периодических решений в нелинейной системе с ограничением. В такой системе имеются три периодических решения с частотами w 01 , w 02 и w 03 , определяемыми в точках пересечения фазовой характеристики y лч (w) с линией -180 0 . Амплитуды периодического решения a 01 , a 02 и a 03 определяются из условия (2.37) по логарифмическим амплитудным характеристикам нелинейного элемента -L э (w 01 , a ), -L э (w 02 , a ) и -L э (w 03 , a ).

Рис. 2.12. Логарифмические амплитудные и фазовая характеристики

Из трех решений, определенных на рис. 2.12, устойчивы два. Решение с частотой w = w 01 и амплитудой a = a 01 устойчиво, так как в диапазоне частот 1, где L лч (w)³-L э (w 01 ,a 01 +Da ), фазовая характеристика y лч (w) не пересекает линию -180 0 , а в диапазоне частот 2, где L лч (w)³-L э (w 01 ,a 01 -Da ), фазовая характеристика y лч (w) один раз пересекает линию -180 0 . Решение с частотой w = w 02 и амплитудой a = a 02 неустойчиво, так как в диапазоне частот, где L лч (w)³-L э (w 02 ,a 02 +Da ), фазовая характеристика y лч (w) один раз пересекает линию -180 0 . Высокочастотное периодическое решение с частотой w = w 03 и амплитудой a = a 03 устойчиво, так как в диапазоне частот, где L лч (w)³-L э (w 03 ,a 03 +Da ), имеется один положительный и один отрицательный переход фазовой характеристики y лч (w) через линию -180 0 , а в диапазоне частот, где L лч (w)³-L э (w 03 ,a 03 -Da ), имеются два положительных и один отрицательный переход фазовой характеристики y лч (w) через линию -180 0 .

В рассмотренной системе при малых по величине возмущениях установятся высокочастотные автоколебания с частотой w 03 и амплитудой a 03 , а при больших по величине возмущениях - низкочастотные автоколебания с частотой w 01 и амплитудой a 01 .

Пример. Исследовать автоколебательные режимы в нелинейной системе, линейная часть которой имеет следующую передаточную функцию

где k=200 c -1 ; T 1 =1.5 c; T 2 =0.015 c,

а в качестве нелинейного элемента используется реле с зоной нечувствительности (рис. 2.4,б) при с=10 В, b=2 В.

Р е ш е н и е. По таблице для реле с зоной нечувствительности находим коэффициенты гармонической линеаризации:

При a ³ b, q¢(a ) = 0.

При построении характеристик нелинейного элемента целесообразно использовать относительное по сравнению с зоной нечувствительности значение амплитуды входного гармонического воздействия m = a /b. Перепишем выражение коэффициента гармонической линеаризации в виде

где - коэффициент передачи реле;

Относительная амплитуда.

Коэффициент передачи реле k н отнесем к линейной части системы и получим нормированные коэффициенты гармонической линеаризации

и нормированную логарифмическую амплитудную характеристику релейного элемента с обратным знаком

Если m ® 1, то -L э (m) ® ¥; а при m >> 1 -L э (m) = 20 lg m. Таким образом, асимптотами нормированной логарифмической амплитудной характеристики с обратным знаком являются вертикальная прямая и прямая с наклоном +20дб/дек, которые проходят через точку с координатами L = 0, m = 1 (рис. 2.13).

Рис. 2.13. Определение периодического решения в релейной системе

с зоной нечувствительности

a 0 = b´m 1 = = 58 В.

Для решения вопроса о существовании автоколебаний в соответствии с нормированной логарифмической амплитудной характеристикой с обратным знаком нелинейного элемента и передаточной функцией линейной части системы

на рис. 2.13 построены логарифмические характеристики L лч (w), -L э (m) и y лч (w).

Частота периодического решения w 0 = 4.3 c -1 определяется в точке пересечения фазовой характеристики y лч (w) и линии -180 0 . Амплитуды периодических решений m 1 = 29 и m 2 = 1.08 находятся по характеристикам L лч (w) и -L э (m). Периодическое решение с малой амплитудой m 2 неустойчиво, а периодическое решение с большой амплитудой m 1 устойчиво.

Таким образом, в исследуемой релейной системе существует автоколебательный режим с частотой w 0 = 4.3 c -1 и амплитудой a 0 = b´m 1 = = 58 В.

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Метод гармонической линеаризации

Методические указания к лабораторной работе по курсу «Теория автоматического управления» для студентов специальности 210100

Одобрено

редакционно –издательским советом

Балаковского интститута техники,

технологии и управления

Балаково 2004

Цель работы: Изучение нелинейных систем с помощью метода гармонической линеаризации (гармонического баланса), определение коэффициентов гармонической линеаризации для различных нелинейных звеньев. Получение навыков по нахождению параметров симметричных колебаний постоянной амплитуды и частоты (автоколебаний), используя алгебраический, частотный способы, а также с помощью критерия Михайлова.

ОСНОВНЫЕ СВЕДЕНИЯ

Метод гармонической линеаризации относится к приближенным методам исследования нелинейных систем. Он позволяет достаточно просто и с приемлемой точностью оценивать устойчивость нелинейных систем, определять частоту и амплитуду установившихся в системе колебаний.

Предполагается, что исследуемая нелинейная САУ может быть представлена в следующем виде

причем нелинейная часть должна иметь одну нелинейность

. (1)

Эта нелинейность может быть как непрерывной, так и релейной, однозначной или гистерезисной.

Любую функцию или сигнал можно разложить в ряд по системе линейно-независимых, в частном случае ортонормированных функций. В качестве такого ортогонального ряда может быть использован ряд Фурье.

Разложим в ряд Фурье выходной сигнал нелинейной части системы

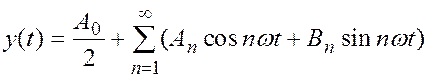, (2)

здесь - коэффициенты Фурье,

,

,

. (3)

Таким образом, сигнал согласно (2) может быть представлен в виде бесконечной суммы гармоник с возрастающими частотами и т. д. Этот сигнал поступает на вход линейной части нелинейной системы.

Обозначим передаточную функцию линейной части

, (4)

причем степень полинома числителя должна быть меньше степени полинома знаменателя. В этом случае АЧХ линейной части имеет вид

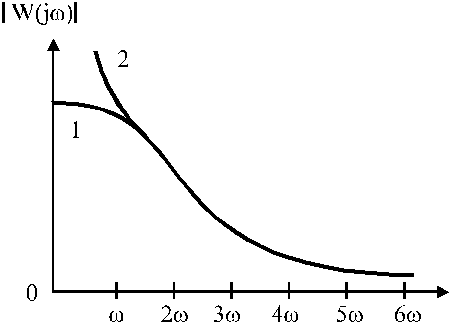
где 1 - не имеет полюсов, 2 - имеет полюс или полюса.

Для АЧХ справедливо записать

Таким образом, линейная часть нелинейной системы является фильтром высоких частот. В этом случае линейная часть будет пропускать без ослабления только низкие частоты, высокие же по мере роста частоты будут существенно ослабляться.

В методе гармонической линеаризации делается предположение о том, что линейная часть системы будет пропускать только постоянную составляющую сигнала и первую гармонику. Тогда сигнал на выходе линейной части будет иметь вид

Этот сигнал проходит по всему замкнутому контуру системы Рис.1 и на выходе нелинейного элемента без учета более высоких гармоник, согласно (2) имеем

. (7)

При исследовании нелинейных систем с помощью метода гармонической линеаризации возможны случаи симметричных и несимметричных колебаний. Рассмотрим случай симметричных колебаний. Здесь и.

Введем следующие обозначения

,

.

Подставив их в (7), получим . (8)

С учетом того, что

,

, где ,

. (9)

Согласно (3) и (8) при

,

. (10)

Выражение (9) является гармонической линеаризацией нелинейности устанавливает линейную связь входной переменной и выходной при . Величины и называются коэффициентами гармонической линеаризации.

Необходимо отметить, что уравнение (9) является линейным для конкретных величин и (амплитуды и частоты гармонических колебаний в системе). Но в целом оно сохраняет нелинейные свойства, так как коэффициенты различны для различных и . Эта особенность и позволяет исследовать с помощью метода гармонической линеаризации свойства нелинейных систем [ Попов Е.П.].

В случае несимметричных колебаний гармоническая линеаризация нелинейности приводит к линейному уравнению

,

,

. (12)

Так же как и уравнение (9), линеаризованное уравнение (11) сохраняет свойства нелинейного элемента, так как коэффициенты гармонической линеаризации , , а так же постоянная составляющая зависят и от смещения и от амплитуды гармонических колебаний .

Уравнения (9) и (11) позволяют получить передаточные функции гармонически линеаризованных нелинейных элементов. Так для симметричных колебаний

Как уже отмечалось, в нелинейных и в особенности релейных АСР часто наблюдаются устойчивые периодические колебания постоянной амплитуды и частоты, так называемые автоколебания . Причем автоколебания могут сохраняться даже при значительных изменениях параметров системы. Практика показала, что во многих случаях колебания регулируемой величины (рис. 3) близки к гармоническим.

Близость автоколебаний к гармоническим позволяет использовать для определения их параметров – амплитуды A и частоты w 0 – метод гармонической линеаризации. В основе метода лежит предположение, что линейная часть системы является фильтром низких частот (гипотеза фильтра). Определим условия, при которых автоколебания в системе могут быть близки к гармоническим. Ограничимся системами, которые как на рис. 3 могут быть приведены к последовательному соединению нелинейного элемента и линейной части. Предположим, что сигнал задания величина постоянная, для простоты примем его равным нулю. А сигнал ошибки (рис 3) является гармоническим:

Выходной сигнал нелинейного элемента как всякий периодический сигнал – на рисунке 3 это прямоугольные колебания – может быть представлен в виде суммы гармоник ряда Фурье.

Допустим, что линейная часть системы является фильтром низких частот (рис. 4) и пропускает только первую гармонику с частотой w 0 . Вторая с частотой 2w 0 и более высокие гармоники отфильтровываются линейной частью. В этом случае на выходе линейной части будет существовать практически только первая гармоника , а влиянием высших гармоник можно пренебречь

Таким образом, если линейная часть системы является фильтром низких частот, а частота автоколебаний w 0 удовлетворяет условиям

, (4)

Предположение, что линейная часть системы является фильтром низких частот, называется гипотезой фильтра . Гипотеза фильтра выполняется всегда, если разность степеней полиномов знаменателя и числителя передаточной функции линейной части

не меньше двух

Условие (6) выполняется для многих реальных систем. Примером могут служить апериодическое звено второго порядка и реальное интегрирующее

При исследовании автоколебаний, близких к гармоническим, в расчет принимается только первая гармоника периодических колебаний на выходе нелинейного элемента, поскольку высшие гармоники все равно практически отфильтровываются линейной частью. В режиме автоколебаний осуществляется гармоническая линеаризация нелинейного элемента. Нелинейный элемент заменяется эквивалентным линейным с комплексным коэффициентом усиления (описывающей функцией) , зависящим от амплитуды входного гармонического сигнала:

где и – действительная и мнимая части ,

– аргумент ,

– модуль .

В общем случае зависит как от амплитуды так и частоты автоколебаний и постоянной составляющей . Физически комплексный коэффициент усиления нелинейного элемента , чаще называемый коэффициентом гармонической линеаризации , есть комплексный коэффициент усиления нелинейного элемента по первой гармонике . Модуль коэффициента гармонической линеаризации

численно равен отношению амплитуды первой гармоники на выходе нелинейного элемента к амплитуде входного гармонического сигнала.

Аргумент

характеризует сдвиг по фазе между первой гармоникой выходных колебаний и входным гармоническим сигналом. Для однозначных нелинейностей, таких как, например, на рис. 2,а и 2,б, действительное выражение и

Для неоднозначных нелинейностей, рис. 2,в, 2,г, определяется по формуле

где S – площадь петли гистерезиса. Площадь S берется со знаком плюс, если петля гистерезиса обходится в положительном направлении (рис. 2,в) и со знаком минус в противном случае (рис. 2,г).

В общем случае и вычисляются по формулам

где , – нелинейная функция (характеристика нелинейного элемента).

С учетом вышеизложенного, при исследовании автоколебаний, близких к гармоническим, нелинейная АСР (рис. 3) заменяется эквивалентной с коэффициентом гармонической линеаризации вместо нелинейного элемента (рис. 5). Выходной сигнал нелинейного элемента на рис. 5 обозначен как , это

Подчеркивает, что нелинейный элемент генерирует только

первую гармонику колебаний. Формулы для коэффициентов гармонической линеаризации для типовых нелинейностей можно найти в литературе, например, в . В таблице приложения В приведены характеристики исследуемых релейных элементов, формулы для и их годографы. Там же приведены формулы и годографы для обратного коэффициента гармонической линеаризации , определяемого выражением

где и действительная и мнимая часть . Годографы и строятся в координатах , и , соответственно.

Запишем теперь условия существования автоколебаний. Система на рис. 5 эквивалентна линейной. В линейной системе существуют незатухающие колебания, если она находится на границе устойчивости. Воспользуемся условием границы устойчивости по критерию Найквиста: . На рис. 6,а – две точки пересечения, что указывает на наличие двух предельных циклов.

Метод гармонической линеаризации позволяет с достаточной для практики точностью исследовать устойчивость и точность нелинейных систем, используя методы, разработанные для линейных систем. Метод дает возможность определить наличие автоколебаний, а также их частоту и амплитуду.

Нелинейная система представляется в виде соединения линейной и нелинейной части (рис. 5).

Рис. 5 Схема нелинейной системы

Выходной сигнал нелинейной части системы в общем случае определяется выражением

Обозначим как передаточную функцию линейной части. Система уравнений примет вид

Найдем условия, при которых на выходе линейной части системы возникают гармонические колебания вида

В этом случае сигнал y(t) нелинейной части будет представлять собой также периодическую функцию, но отличную от синусоиды. Эту функцию можно разложить в ряд Фурье

В этом выражении a i и b i - коэффициенты Фурье. Для симметричных нелинейностей F 0 =0.

Основным условием, которое накладывает метод на линейную часть системы, является условие фильтра нижних частот. Считается, что линейная часть пропускает только первую гармонику колебаний. Данное допущение позволяет считать высшие гармоники в (7.19) несущественными и ограничиться рассмотрением только первой гармоники сигнала y(t).

то выражение (7.20) можно переписать в виде

Первое уравнение системы (7.17) примет вид

В этом выражении

Результат замены нелинейности F(x,sx) выражением

и называется гармонической линеаризацией. Величины q и q 1 называются коэффициентами гармонической линеаризации или просто гармоническими коэффициентами. Для однозначных нелинейностей обычно q 1 =0 . Формулы для гармонических коэффициентов, соответствующих типовым нелинейностям, приводятся в приложениях.

Принципиальное отличие гармонической линеаризации от обычной состоит в том, что при обычной линеаризации нелинейную характеристику заменяют прямой линией с определенной постоянной крутизной, а при гармонической линеаризации - прямой линией, крутизна которой зависит от амплитуды входного сигнала нелинейного элемента.

Рассмотрим методику определения амплитуды и частоты автоколебаний.

1). В характеристическом уравнении системы, полученном из (7.22) делаем замену s=j и получим

2). Из полученного выражения выделяем вещественную и мнимую части и приравниваем их нулю, что, по критерию Михайлова, соответствует нахождению системы на колебательной границе устойчивости.

• 3).Решение этой системы дает частоту и значения гармонических коэффициентов. Если эти значения вещественны и положительны, то в системе существует предельный цикл. По значениям гармонических коэффициентов можно определить амплитуду предельного цикла.
• 4). Общим признаком устойчивости предельного цикла, т.е. существования автоколебаний, является равенство нулю предпоследнего определителя Гурвица при полученных значениях амплитуды и частоты предельного цикла. Часто более удобно использовать условие устойчивости предельного цикла, в основе которого лежит критерий устойчивости Михайлова.

Если это неравенство выполняется, то предельный цикл устойчив и в системе существуют автоколебания с определенными выше амплитудой и частотой. Индекс ”*” означает, что производные вычислены при уже известных значениях гармонических коэффициентах, амплитуды и частоты.

Пример. Допустим, что в уже рассмотренной выше системе стабилизации угла тангажа самолета рулевой привод нелинейный и его структурная схема имеет вид, показанный на рис. 7.6.

Рис.6 Схема нелинейного рулевого привода

Зададим следующие параметры нелинейности скоростной характеристикм рулевого привода: b = 0.12, k 1 = tg =c/b = 6.7. Коэффициенты гармонической линеаризации этой нелинейности определяются выражениями

Заменив в схеме нелинейную характеристику гармоническим коэффициентом, получим передаточную функцию рулевого привода

Подставим эту передаточную функцию в структурную схему системы стабилизации угла тангажа и определим передаточную функцию замкнутой системы

В характеристическом уравнении замкнутой системы сделаем замену s = j и выделим вещественную и мнимую части.

Из второго уравнения системы получим выражение для частоты: , и подставив его в первое уравнение, после преобразований получим

Подставив сюда ранее определенные выражения для коэффициентов характеристического уравнения, можно получить квадратное уравнение относительно гармонического коэффициента, решив которое, найдем

По этим значениям можно вычислить для двух случаев все коэффициенты характеристического уравнения и определить частоты, соответствующие каждому значению q(А). Получим:

Оба значения гармонического коэффициента и соответствующие частоты вещественны и положительны. Следовательно, в системе существуют два предельных цикла. Значения амплитуды предельного цикла определяются численно путем подбора такого значения при котором формула для коэффициента гармонической линеаризации дает значение, равное ранее вычисленному. В рассматриваемом случае получим

Теперь оценим устойчивость предельных циклов. Используем неравенство, полученное из критерия Михайлова, для чего определим

Производная от коэффициента гармонической линеаризации, входящая в полученные выражения, вычисляется по формуле

Расчеты по выше приведенным формулам показывают, что первый предельный цикл не устойчив и возникает он при (0) 0.1166(6.7 0 ). Если начальное отклонение меньше указанного, то процесс на входе нелинейного элемента затухает (рис.7. 7) и система устойчива.

Если начальное значение угла тангажа больше указанного, то процессы сходятся ко второму предельному циклу, который устойчив и, таким образом в системе возникают автоколебания (рис. 8).

Рис. 8

Путем моделирования определено, что область притяжения устойчивого предельного цикла лежит приблизительно в пределах (0) 0.1167 - 1.4 (6.71 0 - 80.2 0 ).